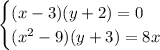
Так как произведение равно нулю когда один из множителей равен нулю, то систему можно представить в виде совокупности двух систем:
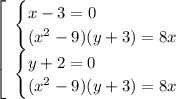
Решаем первую систему.
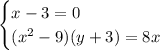
Из первого уравнения получим:

Подставим во второе:
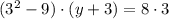
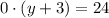
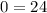
Получили неверное равенство. Уравнение не имеет решений. Значит и первая система не имеет решений.
Решаем вторую систему.
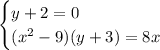
Из первого уравнения получим:
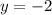
Подставим во второе уравнение:
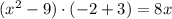
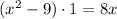
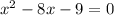
Так как сумма старшего коэффициента и свободного члена равна второму коэффициенту, то корни уравнения:
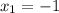
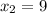
ответ: (-1; -2); (9; -2)
а⁴ + b⁴ ≥ а³b + аb³
1)
а⁴ + b⁴ - а³b - аb³ ≥ 0
а³(а-b) - b³(а-b) ≥ 0
(а-b)(а³-b³) ≥0
(а-b)(а-b)(а²+аb+b²) ≥0
(а-b)²·(а²+аb+b²) ≥0
2)
Первая скобка всегда больше или равна 0, остаётся доказать, что вторая скобка тоже всегда больше или равна 0.
а²+аb+b² ≥0
a) Докажем для неотрицательных a и b.
(a²+ab+ab+b²)-ab ≥ 0
(a² + 2ab + b²) ≥ ab
(a+b)² ≥ ab
а+b ≥ √аb
Это неравенство справедливо как следствие из теоремы Коши для среднего арифметического и среднего геометрического:
(а+b)/2 ≥ √аb
Таким образом, всегда справедливо неравенство во второй скобке
(a²+ab+b²) ≥ 0.
2) Докажем справедливость неравенства (a²+ab+b²) > 0 для отрицательных значений a и b.
a<0; b<0
a²>0; b²>0 - первое и третье слагаемые a² и b² всегда положительны
ab>0, как произведение двух отрицательных(минус × минус = плюс)
Сумма положительных слагаемых тоже положительна:
(a²+ab+b²) > 0
3) Докажем справедливость неравенства (a²+ab+b²) > 0 для значений a и b, различных по знаку: a>0; b<0.
(a²+ab+ab+b²)-ab > 0
(a² + 2ab + b²) > ab
(a+b)² > ab
Это неравенство справедливо, т.к.
(a+b)² ≥ 0
ab < 0 (плюс × минус = минус)
Положительное число больше отрицательного.
Таким образом все три варианта доказывают справедливость неравенства
(а²+ab+b²)≥0. Что и требовалось доказать.