![x^3+3x+2\sqrt[3]{x-4} -34=0](/tpl/images/1360/1028/6c477.png)
Запишем уравнение в виде:
![x^3+3x -34=-2\sqrt[3]{x-4}](/tpl/images/1360/1028/bd4bd.png)
Пусть левая и правая часть равны у. Тогда получим систему:
![\begin{cases} y=x^3+3x -34\\y=-2\sqrt[3]{x-4}\end{cases}](/tpl/images/1360/1028/c1e6e.png)
Рассмотрим каждое уравнение как функцию.
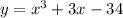- возрастающая функция, так как это кубическая парабола с положительным старшим коэффициентом
![y=-2\sqrt[3]{x-4}](/tpl/images/1360/1028/0df79.png)
- убывающая функция, так как корень нечетной степени имеет сомножителем отрицательное число
Графически возрастающая и убывающая функция могут пересекаться не более чем в одной точке.
В данном случае, понимая, что и область определения и область значений каждой функции представляют собой все действительные числа можно сказать, что такое пересечение обязательно произойдет.
Таким образом, если найден некоторый корень этого уравнения, то других корней у уравнения нет.
Подберем корень. Удобно начать проверку с "красивых значений". Например, будем выбирать х так, чтобы под знаком корня получался куб некоторого целого числа.
Пусть ![\sqrt[3]{x-4} =\sqrt[3]{0}](/tpl/images/1360/1028/d91f8.png)
, то есть 
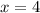. Проверим, является ли это число корнем:
![4^3+3\cdot4+2\sqrt[3]{4-4} -34=64+12+2\cdot0-34=42\neq 0](/tpl/images/1360/1028/6e40b.png)
- не корень
Пусть ![\sqrt[3]{x-4} =\sqrt[3]{1}](/tpl/images/1360/1028/7bd4a.png)
, то есть 
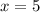. Проверим, является ли это число корнем:
![5^3+3\cdot5+2\sqrt[3]{5-4} -34=125+15+2\cdot1-34=108\neq 0](/tpl/images/1360/1028/f1f89.png)
- не корень
Пусть ![\sqrt[3]{x-4} =\sqrt[3]{-1}](/tpl/images/1360/1028/4572f.png)
, то есть 
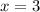. Проверим, является ли это число корнем:
![3^3+3\cdot3+2\sqrt[3]{3-4} -34=27+9+2\cdot(-1)-34=0](/tpl/images/1360/1028/fd423.png)
- корень
Таким образом, уравнение имеет единственный корень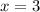
ответ: 3
«Молитва это вульгаризованная и рационалистически разжиженная позднейшая форма чего-то очень энергичного, активного и сильного: магического заклинания, принуждения бога» (Т. Манн)
Самая первая, самая красивая, мелодичная часть этой повести – молитва героя. Именно такая молитва, не тихая христианская но убеждение, заклинание, попытка слабого, потерянного человека принудить судьбу измениться. Во имя его любви.
При том, такой любви, в которую очень поверить первой любви, в которой разом встретилась та самая девушка, румяная, взволнованная, очень юная «Она» – и еще весна, цветущие деревья, красота мира, воспринятая молодой, впечатлительной душой, и еще вера в светлое будущее, наивная за него борьба. Все то, что было у него и все, что отняли разом. Сама жизнь, которую он потерял, которую нельзя уже вернуть, но он верит, что можно, с одной единственной нити, с Нее, в образ которой измученно сердце соединило все светлое, что сумело сохранить.
Но Бог, в которого герой никогда прежде не верил, конечно, не внемлет молитве и карает героя за нее, не то чтобы жестоко стирает с лица земли, прекращая разом и надежды и муки. Вообще, у Грина очень интересен мотив «молитвы», она предстает, как заклинание, которое может читать лишь избранный. Для всех же остальных это слабость, непозволительное покушение на божественные сферы. Так и здесь. Молитва сломанного тюрьмой человека, искренняя, жалобная, тихая, у которой недостаточно силы, чтобы заставить Бога покориться человеческой воле.
«У него была одна молитва, только одна…»
ответ: n=12.
Объяснение:
а₁=-4 d=2 Sn=84 n=?
Sn=(2*a₁+(n-1)*d)*n/2
(-4*2+(n-1)*2)*n/2=84
(-8+(n-1)*2)*n/2=84 |×2
(-8+2n-2)*n=168
(2n-10)*n=168
2n²-10n-168=0 |÷2
n²-5n-84=0 D=361 √D=19
n₁=12 n₂=-7 ∉
ответ: n=12.