1) Установить соответствие:
Угол ABC опирается на дугу ADC
Угол DEF опирается на дугу DCF
Угол AGF опирается на дугу ACF
2) Условно примем, что хорда АВ разделилась на отрезки АМ=25 см и ВМ=36 см. Тогда отношение частей хорды CD будет равно СМ/MD=1/4. Отрезки двух хорд связаны: произведение отрезков одной хорды равно произведению отрезков другой хорды.
Примем за х одну часть. Тогда СМ будет равен х, а MD - 4х. Составляем уравнение:
25*36=х*4х
900=4х^2
х^2=900/4
х^2=225
х=15
Находим 4х:
4*15=60 см.
Длина второй хорды равна 15+60=75 см. Следовательно, верный ответ 4 - 75 см.
3) Верный высказывания: 2 и 3.
Второе высказывание верно, потому что при делении числа на два не может быть двух разных результатов.
Третье высказывание верно, потому что градусная мера полуокружности равна 180 градусам, а вписанный угол равен половине градусной меры дуги, на которую опирается. Следовательно, вписанный угол, опирающийся на полуокружность, будет равен 180/2=90 градусов.
4) Определение вписанного угла: угол, стороны которого пересекают окружность, а вершина лежит на окружности, является вписанным. Следовательно, нужными пунктами будут 1 и 5.
5) Вписанными углами будут являться углы под номерами 1, 2 и 5.
6) Угол ABC - вписанный, значит градусная мера дуги, на которую он опирается, будет равна удвоенной градусной мере угла: 44*2=88 градусов.
Также указано, что дуга AB равна 92 градуса. Учитывая то, что вся окружность равняется 360 градусам, составляем уравнение:
Дуга BC=360-(88+92)
Дуга BC=360-180
Дуга ВС=180 градусов.
7) Из рисунка видно, что BC - это диаметр, следовательно, дуга BAC будет равна 180 градусов. Известно, что часть дуги ВАС - дуга ВА равна 100 градусам, значит вторая часть - дуга АС будет равна 180-100=80 градусов.
Угол ABC - вписанный, значит его градусная мера равна половине градусной меры дуги, на которую он опирается: 80/2=40 градусов.
8) Дуги АВ и ВС соприкасаются в точке В, значит дуга АВ+дуга ВС=дуга АВС; 152+80=232 градусов.
Дуга АС равна 360- 232= 128 градусов.
Угол AВС - вписанный, значит его градусная мера равна 128/2=64 градуса.
Объяснение:
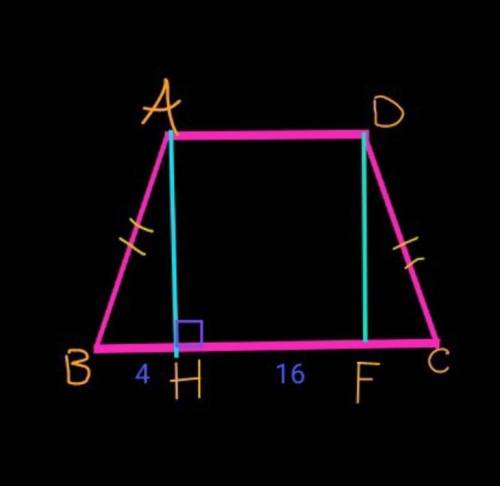
№8
Дано:
АН – высота;
ВН=4 дм;
НС=16 дм;
АВ=DC.
Проведём высоту DF к стороне ВС.
Рассмотрим прямоугольные треугольники АНВ и DFC.
АВ=DC по условию;
Так как основания трапеции паралельны, а АН и DF высоты, проведенные к основанию ВС, то АDFH прямоугольник. Следовательно АН и DF равны.
Тогда прямоугольные треугольники АНВ и DFC равны по гипотенузе и катету. Следовательно FC=BH=4;
HF=HC–FC=16–4=12 (дм).
Так как АDFH – прямоугольник (доказано ранее), то AD=HF=12 (дм)
ответ: Б) 12 дм.
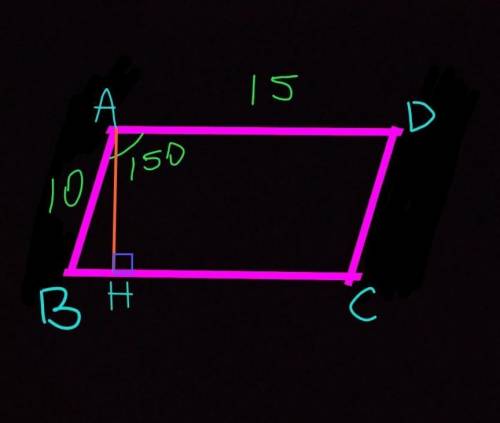
№9
Рассмотрим треугольник АВН.
Так как АН – высота (по условию), то угол АНВ=90, тогда треугольник АВН прямоугольный.
Сумма углов при одной его стороне равна 180°, тогда:
угол ABH= 180°– угол BAD=180°–150°=30°
В прямоугольном треугольнике напротив угла в 30° лежит катет вдвое меньший гипотенузы, тоесть:
АН=АВ÷2=10÷2=5 см.
S=ah, где S–площадь паралелограмма, а– сторона паралелограмма, h– высота паралелограмма.
Подставим значения:
S=15*5=75 см²
ответ: В) 75 см²
a) 3x⁸ - x³ - x⁸ + 6x - 2x⁸ - 1 = -x³ + 6x - 1
б) xy + 12x⁵y - 10x⁵y - 6 -2x⁵y = xy - 6
в) 4x³ - 2x² + 3 - 4x³ + 2x² = 3
г) 2x - 2xy² + 2y - x - y + 2xy² + 3 = x + y + 3
д) x²y - xy² - x²y + xy² = 0