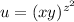 . Как найти производную функции относительно
. Как найти производную функции относительно  , то есть
, то есть 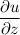 . Как я понимаю,
. Как я понимаю,  и
и 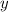 в данном случае считаем константами. Значит получаем число в степени
в данном случае считаем константами. Значит получаем число в степени 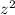 . Что с ним делать не знаю.
. Что с ним делать не знаю.14х(х-4) - (х+1)(9х-30) 14х²-56х-9х²+30х-9х+30
< 0 < 0
(х+1)(х-4) (х+1)(х-4)
5х²-35х+30 5(х-6)(х-1)
< 0 < 0
(х+1)(х-4) (х+1)(х-4) Нули: -1; 1; 4; 6
+ - + - +
оооо>
-1 1 4 6
ответ: (-1;1)U(4;6)
б) a+b-a^2+b^2=
= (a+b)-(a^2-b^2)=
=(a+b)-(a-b)(a+b)=
=(a+b)(1-a+b)
г) m-m^2-n+n^2=
=(m-n)-(m^2-n^2)=
=(m-n)(1-m-n)
б) b^2-bc-a^2+ac=
=-a^2+ab-ab+b^2+ac-bc=
=-(a^2-ab)-(ab-b^2)+(ac-bc)=
=-a(a-b)-b(a-b)+c(a-b)=
=(a-b)(c-a-b)
г) - не понятная запись
б) xy^2+x^2y-x^3-y^3=
=(xy^2-y^3)-(x^3-x^2y)=
=y^2(x-y)-x^2(x-y)=
=(y^2-x^2)(x-y)=
=(y-x)(y+x)(x-y)
г) a^3-3a^2b+3ab^2-b^3=
=(a^3-b^3)-(3a^2b-3ab^2)=
=(a-b)(a^2+ab+b^2)-(a-b)3ab=
=(a^2+ab+b^2-3ab)(a-b)=
=(a^2-2ab+b^2)(a-b)=
=(a-b)^2(a-b)=
=(a-b)^3
(xy)**(z**2) × ln (xy) × 2 × z
Объяснение:
да, x и y считаем константами, и получается функция вида:
a**x
(a**x)' = a**x × ln a
в нашем случае надо еще продифференцировать z**2.
частная производная по z:
((xy)**(z**2))'= (xy)**(z**2) × ln (xy) × (z**2)' = (xy)**(z**2) × ln (xy) × 2 × z