В решении.
Объяснение:
Дана функция у= -х² - 4х + 4;
a) координаты вершин параболы;
1) Найти х₀:
Формула: х₀ = -b/2a;
у= -х² - 4х + 4;
х₀ = 4/-2
х₀ = -2;
2) Найти у₀:
у= -х² - 4х + 4;
у₀ = -(2²) - 4*(-2) + 4 = -4 + 8 + 4 = 8
у₀ = 8;
b) ось симметрии параболы;
Ось симметрии Х = х₀
Х = -2;
c) точки пересечения параболы с осью Ох;
Точки пересечения параболы с осью Ох называются нулями функции (у в этих точках равен нулю).
Приравнять уравнение функции к нулю и решить квадратное уравнение:
-х² - 4х + 4 = 0/-1
х² + 4х - 4 = 0
D=b²-4ac = 16 + 16 = 32 √D=√16*2 = 4√2
х₁=(-b-√D)/2a
х₁=(-4-4√2)/2
х₁= -2 - 2√2 ≈ -4,8;
х₂=(-b+√D)/2a
х₂=(-4+4√2)/2
х₂= -2 + 2√2 ≈ 0,8;
х₁= -2 - 2√2; х₂= -2 + 2√2 - нули функции.
d) точки пересечения параболы с осью Оу;
Любой график пересекает ось Оу при х = 0:
у= -х² - 4х + 4;
у = -0² - 4*0 + 4
у = 4;
Парабола пересекает ось Оу при у = 4;
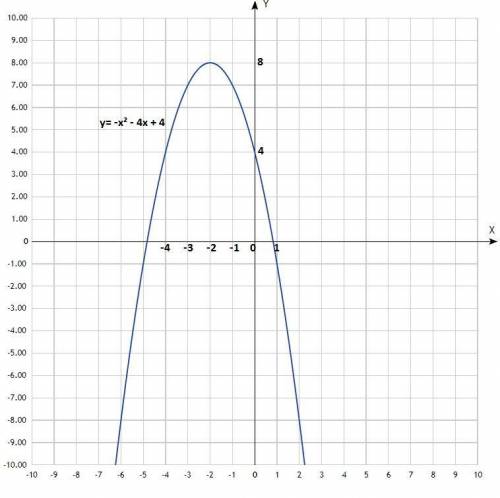
e) постройте график функции;
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х₁= -2 - 2√2 ≈ -4,8 и
х₂= -2 + 2√2 ≈ 0,8.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у= -х² - 4х + 4;
Таблица:
х -6 -5 -4 -3 -2 -1 0 1 2
у -8 -1 4 7 8 7 4 -1 -8
По вычисленным точкам построить параболу.
а2 + а4 + а6 = 33
а2*а4*а6 = 935
распишем 1 уравнение:
а1 + d +a1 +3d +a1 +5d = 33
3a1 + 9d = 33
a1 + 3d = 11
выразим а1
a1 = 11 - 3d
распишем 2 уравнение:
(а1 + d)(a1 +3d)(a1 + 5d) = 935
заменим а1:
(11 - 3d +d)(11 - 3d +3d)(11 - 3d +5d) = 935
11(11 - 2d)(11 + 2d) =935
(11 - 2d)(11 +2d) = 85
в скобках формула разности квадратов:
121 - 4d^2 = 85
4d^2 = 36
d^2 = 9
т.к. прогрессия возрастающая, то d = 3
находим первый член:
а1 = 11- 3*3=11-9=2
находим разность:
a6 - a4 - a2=a1 +5d - a1 - 3d -a1 - d=d - a1 = 3 - 2 = 1
произведение:
a1*(a6 - a4 - a2)= 2*1=2
(-0,5x^4y)*(16x^4y^3)^2=(-0,5x^4y)*256x^8y^6= -128x^12y^7.