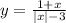
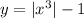
Складемо рівняння для визначення чисельника початкового дробу,позначивши його через x (x > 0).
тоді знаменник дорінює (х+7), дріб х/(х+7), якщо чисельник цього дробу зменшити на 1, а знаменник збільшити на 4, то дріб дорівнюватиме (х-1)/(х+11)
Згідно умови задачі маємо таке рівняння.
х/(х+7)- (х-1)/(х+11)=1/6
6*(х²+11х-х²-7х+х+7)=х²+11х+7х+77
-30х-42+х²+18х+77=0
х²-12х+35=0 За теоремою Вієта х=5 , х=7
Таким чином, чисельник початкового дробу дорівнює 5, дріб 5/12,
перевіримо 5/12-4/16=5/12-1/4=5/12-3/12=2/12=1/6. вірно.
або 7, дріб 7/14, якщо його скоротити, то не виконується умова. але перевіривши 7/14-6/18=1/2-1/3=1/6, тому дріб 7/14 підпадає під відповідь.
Відповідь. 7/14 або 5/12
Решение системы уравнений х₁=5 х₂= -6 х₃=6
у₁=1 у₂= -10 у₃=2
Объяснение:
Решить систему уравнений
(x-5y)(x²-36)=0
x-y=4
Выразим х через у во втором уравнении:
х=4+у
Первые скобки приравняем к нулю, как один из множителей, дающих в результате ноль:
x-5y=0
Подставим выраженное х через у:
4+у-5у=0
4-4у=0
-4у= -4
у= -4/-4
у₁=1
Теперь подставляем значение у в уравнение первых скобок и вычисляем х:
x-5y=0
х=5у
х=5*1
х₁=5
Теперь приравняем к нулю вторые скобки, как один из множителей, дающих в результате ноль:
x²-36=0
x²=36
х₂,₃=±√36
х₂= -6
х₃=6
x-y=4
-у=4-х
у=х-4
у₂=х₂-4
у₂= -6-4
у₂= -10
у₃=х₃-4
у₃=6-4
у₃=2
Решение системы уравнений х₁=5 х₂= -6 х₃=6
у₁=1 у₂= -10 у₃=2