Когда Лермонтов отбывал ссылку на Кавказе, однажды он столкнулся с монахом, который рассказал поэту историю своей жизни. Он поведал писателю, как в детстве был захвачен в плен генералом, как заболел, и его оставили у монахов. Его не оставляла мысль о свободе, и плененный горец делал неоднократные попытки убежать в горы. Есть вероятность того, что этот рассказ и взят в основу сюжета произведения.
В поэме использован и местный фольклор: в одном из эпизодов, где происходит схватка юноши с барсом, основой послужила грузинская песня, героями которой были молодой юноша и тигр.
Год написания поэмы – 1839, она претерпела много редактирований, чтобы пройти через цензуру. Поэту пришлось убрать много фрагментов из глав, где особенно сильно воспевалась свобода, а также, где были ярко выраженные антиправославные эпизоды.
Подробнее: https://obrazovaka.ru/sochinenie/mcyri/analiz-poemy-lermontova.html
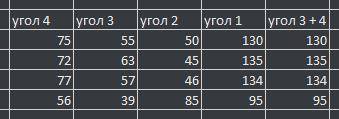
1) ∠2 = 180° - 75° - 55° = 50°
∠1 = 180° - ∠2 = 130°
∠3 + ∠4 = 130°
2) ∠2 = 180° - 135° = 55°
∠4 = 180° - 55° - 63° = 62°
∠3 + ∠4 = 135°
3) ∠3 = 180° - 77° - 46° = 57°
∠1 = 180° - 46° = 134°
∠3 + ∠4 = 134°
4) ∠4 = 180° - 39° - 85° = 56°
∠1 = 180° - 85° = 95°
∠3 + ∠4 = 95°
Объяснение:
Для начала надо знать что сумма всех углов любого треугольника равна 180 градусам, тогда всегда ∠ 2 + ∠ 3 + ∠ 4 = 180 градусам, а ∠ 1 внешний угол треугольника и всегда будет равен 180 - ∠ 2, а ∠ 3 + ∠ 4 ну это просто данное, так что сначала считаешь все углы и находишь одно из другого, а потом считаешь ∠ 3 + ∠ 4.
Итог:
1) ∠2 = 180° - 75° - 55° = 50°
∠1 = 180° - ∠2 = 130°
∠3 + ∠4 = 130°
2) ∠2 = 180° - 135° = 55°
∠4 = 180° - 55° - 63° = 62°
∠3 + ∠4 = 135°
3) ∠3 = 180° - 77° - 46° = 57°
∠1 = 180° - 46° = 134°
∠3 + ∠4 = 134°
4) ∠4 = 180° - 39° - 85° = 56°
∠1 = 180° - 85° = 95°
∠3 + ∠4 = 95°
И это такое посредственное доказательство что внешний угол в треугольнике равняется сумме двух других углов.
1. S(км) V(км/ч) t(ч)
По течению 45 v+2 45/v+2
Против течения 45 v-2 45/v-2
Пусть v - собственная скорость лодки.
(45/v+2)+(45/v-2 )=14
Домножим 1 скобку на (v-2) 2 на (v+2), 14 на (v+2)(v-2)
((45v-90+45v+90)-(14*(v-2)(v+2)))/(v-2)(v+2)=0
-14v^2+90v+56=0 (v-2)(v+2)не=0
Разделим обе части на -2 vне=2; vне=-2
7v^2-45v-28=0
D=(-45)^2-4*7*(-28)=2809.
v1=(45+53)/14=7.
v2=(45-53)/14=-8/14
Т.к. скорость не может быть отрицательной, следовательно собственная скорость лодки равна 7 км/ч.
---
3. 1катет=х(см)
2катет=х+31(см)
гипотенуза=41(см)
По теореме Пифагора:
х^2+(x+31)^2=41^2
x^2+x^2+62x+961=1681
2x^2+62x-720=0
Разделим на 2:
x^2+31x-360=0
D=31^2-4*1*(-360)=2401.
x1=(-31+49)/2=9.
X2=(-31-49)/2=-40
Т.к. длина не может быть отрицательной, следовательно длина 1катета равна 9(см).
Длина 2катета=х+31
31+9=40(см)
1катет=9см, 2катет=40см.