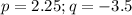Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
∪AC = π = 2·∪AB ⇒ ∪AB = 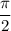
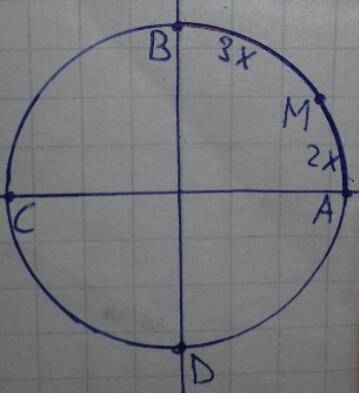
Пусть ∪AM =  , тогда ∪MB =
, тогда ∪MB = 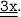
Т.к. первая четверть это ∪AB.
∪AM + ∪MB = 2x+3x = 5x = 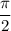 ⇒
⇒
x = 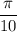 ⇒
⇒ 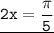 ;
; 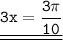
∪DM = ∪DA + ∪AM = 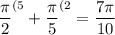
∪MC = ∪MB + ∪BC = 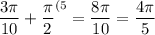
ответ: длина ∪AM = 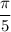
длина ∪MB = 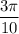
длина ∪DM = 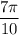
длина ∪MC = 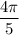
в)
Выразим из второго уравнения системы какую-нибудь неизвестную. Например,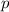 . Для этого перебросим всё, что не имеет отношения к
. Для этого перебросим всё, что не имеет отношения к 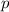 , направо, изменив знак на противоположный по правилам уравнения:
, направо, изменив знак на противоположный по правилам уравнения:
Освободим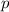 , разделив на 3 обе части уравнения.
, разделив на 3 обе части уравнения.
Теперь подставим выраженное из второго уравнения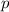 в первое. Получим:
в первое. Получим:
Решаем как обычное линейное уравнение с одной неизвестной.
Теперь находим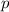 , используя ранее подставленное нами выражение.
, используя ранее подставленное нами выражение.
ответ: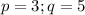
---
г)
Точно такой же подход.
А теперь подставим полученное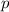 в первое выражение.
в первое выражение.
Разделим всё на -2 для удобства.
Находим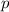 по выведенному ранее выражению.
по выведенному ранее выражению.
ответ: