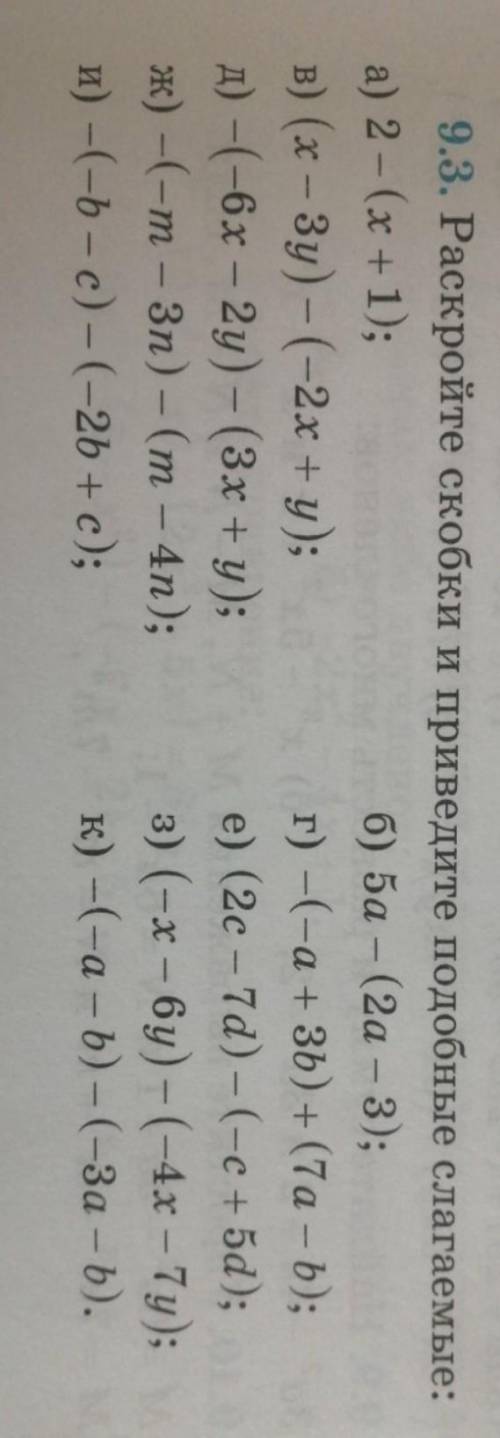
1.
2x-5y при x=7; y=3
2×7-5×3
14-15= -1
ответ: -1
2.
3+2a = -3+2a при a=11
3+3= -2а+2а
6=0 не тождество т.к 6> 0
ответ: 3+2a > -3+2a
3.
1) 8y-4,4y = 3,6у
2)15a-a+b-6b = 15а-1а+1b-6b=14a+(-5b) = 14a-5b
3)2a+(3a-8b)= 2a+3a-8b = 5a-8b
4)(5-2b)-(7+10b) = 5-2b-7-10b = 5-7-2b-10b =-2-12b
5)(2-4b)-(31b-6)-11 = 2-4b-31b+6-11 = 2+6-11-4b-31b = -3-35b
4.
1)3x+2=0
3x=0-2
3x= -2
x= -2/3
2)8x-5=x-40
8х-х=5-40
7х=-35
х=5
3)6x+(3x-2)=14
6х+3х-2=14
9х=2+14
9х=16
х= 1 целая 7/9
объяснение:
если непонятно что-то , то напиши в комментариях
ответ 1:
Функция возрастает на интервале (-1; +∞)
Убывает на (-∞; -1)
Объяснение 1:
через производную:
f'(x)=4x³+4
приравниваем производную к нулю и ищем корни
4x³+4=0
4x³=-4
x³=-1
x=-1 - корень
отмечаем полученные корни на числовой прямой:
[-1]>ₓ
получаются 2 интервала (слева и справа от -1). Берем пробную точку, например 0 (она находится правее чем -1), подставляем в нашу производную f'(x)=4x³+4
f'(0)=4*0³+4=4
получили положительное число (то есть со знаком +), значит правый промежуток с плюсом.
Теперь берем любую точку левее -1, например -2
f'(-2)=4*(-2)³+4=4*(-8)+4=-28 - отрицательное число, значит левый промежуток с минусом, то есть
[-1]>ₓ
Там где производная отрицательна - функция убывает.
Где производная положительна - функция возрастает.
x=-1 - точка минимума (так как до нее функция убывала, а после нее начала возрастать)
///
ответ 2:
Функция f(x) убывает на всё промежутке х ∈ (-∞; +∞)
Объяснение 2:
f(x) = 8 - 4x - x³
Функция определена при х ∈ (-∞; +∞)
Пусть х₂ > x₁
f(x₁) = 8 - 4x₁ - x₁³
f(x₂) = 8 - 4x₂ - x₂³
f(x₂) - f(x₁) = 8 - 4x₂ - x₂³ - (8 - 4x₁ - x₁³) = -4(x₂ - x₁) - (x₂³ - x₁³)
Поскольку х₂ > x₁ , то (x₂ - x₁) > 0 и (x₂³ - x₁³) > 0, тогда
f(x₂) - f(x₁) < 0 , то есть функция f(x) убывает
на всём промежутке х ∈ (-∞; +∞)
Объяснение:
а) = 2-х-1= 1-х
б) = 5а-2а+3= 3а+3
в) = х-3у+2х-у=3х-4у
г) = +а-3b+7a-b= 8a-4b
д)= 6х+2у-3х-у= 3х+у
е) = 2c-7d+c-5d= 3c-12d
ж) = m+3n-m+4n = 7n
з) = -х-6у+4х+7у= 3х +у
и) = b+c+2b-c= 3b
к) = a+b+3a+b= 4a+2b