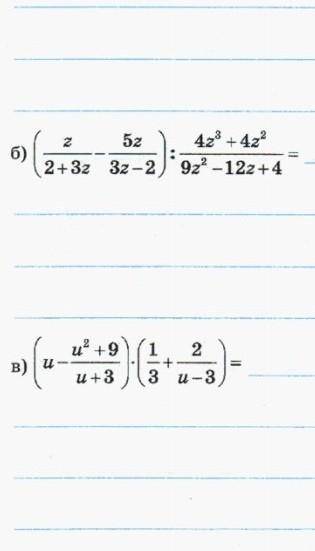
силий Тёркин»? Назовите подзаголовок поэмы. 3. Почему поэт пишет, что «на войне сюжета нету» и что книга «без начала и конца»? 4. Во для анализа главы «Переправа»: а) На какие части разделяют главу слова «Переправа, переправа...»? Каким настроением проникнута каждая часть главы? С какой интонацией следует читать эти строки? б) Что является «лейтмотивом» данной главы? Почему? в) Каким в этой главе предстаёт перед читателем Василий Тёркин? 5. Во для анализа главы «О награде»: а) Как построена эта глава? Дайте характеристику частей этой главы? б) Как проявляется здесь стилевое многообразие поэмы? в) Что нового об образе Тёркина мы узнаём в этой главе? г) Можем ли сказать, что автор сроднился с Тёркиным? В чём это проявляется? Что значит слово «родина» для каждого из них? е) Выделите в главе строки, которые являются рефреном произведения. Как вы думаете, почему именно такой рефрен включён Твардо
Объяснение:
Чтобы выполнить сложение или вычитание алгебраических дробей с одинаковыми знаменателями, надо найти сумму или разность числителей, а знаменатель оставить без изменений.
Пример 1. Выполните сложение алгебраических дробей:
а) a + 3 + a - 3 б) 2b - 1 + b + 4
b b 2 2
Решение: складываем числители дробей и выполняем приведение подобных членов (если они есть):
а) a + 3 + a - 3 = (a + 3) + (a - 3) = a + 3 + a - 3 = 2a
b b b b b
б) 2b - 1 + b + 4 = (2b - 1) + (b + 4) = 2b - 1 + b + 4 = 3b + 3
2 2 2 2 2
Пример 2. Выполните вычитание алгебраических дробей:
а) x + 5 - 5x б) a + b - a + 4
3 3 a - 5 a - 5
Решение: вычитаем из числителя первой дроби числитель второй дроби и выполняем приведение подобных членов (если они есть):
а) x + 5 - 5x = x + 5 - 5x = 5 - 4x
3 3 3 3
б) a + b - a + 4 = (a + b) - (a + 4) = a + b - a - 4 = b - 4
a - 5 a - 5 a - 5 a - 5 a - 5
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями в виде общих формул:
a + b = a + b и a - b = a - b (c≠0)
c c c c c c
Если дроби имеют знаменатели, состоящие из противоположных выражений, то есть выражений, отличающихся только знаком, надо тождественно преобразовать одну из дробей, чтобы привести их к общему знаменателю. Преобразование выполняется в соответствии с правилами знаков:
a = -a
b -b
Данное преобразование можно рассматривать как умножение числителя и знаменателя дроби на -1. Следовательно, если числитель и знаменатель алгебраической дроби заменить на противоположные выражения, то получится дробь, равная данной. Полученную дробь можно переписать, поставив один из минусов перед дробью:
a = -a = - a = - -a
b -b -b b
Также, любую отрицательную дробь можно сделать положительной, перенеся минус, стоящий перед дробью, в числитель или знаменатель:
- a = -a = a
b b -b
Пример 1. Найдите сумму дробей:
5a + 3a
b - c c - b
Решение: чтобы выполнить сложение, поменяем знаки перед второй дробью и в её знаменателе на противоположные:
5a + 3a = 5a - 3a = 5a - 3a = 2a
b - c c - b b - c -(c - b) b - c b - c b - c
Пример 2. Найдите разность дробей:
n + 5 - 2n
n2 - m m - n2
Решение: чтобы выполнить вычитание, перенесём знак минус, стоящий перед второй дробью, в её знаменатель:
n + 5 - 2n = n + 5 + 2n = n + 5 + 2n = 3n + 5
n2 - m m - n2 n2 - m -(m - n2) n2 - m n2 - m n2 - m
Сложение и вычитание с разными знаменателями
Чтобы найти сумму или разность алгебраических дробей с разными знаменателями, надо:
найти общий знаменатель,
привести алгебраические дроби к общему знаменателю,
выполнить сложение или вычитание,
сократить полученную дробь, если это возможно.
Пример 1. Выполните сложение дробей:
2a + b
a + b a - b
Решение: находим общий знаменатель. Он будет равен произведению знаменателей данных дробей:
(a + b)(a - b)
Как находить общий знаменатель, Вы можете узнать на странице Приведение алгебраических дробей к общему знаменателю. Далее умножаем числитель каждой дроби на дополнительный множитель:
2a(a - b) = 2a2 - 2ab
b(a + b) = ab + b2
Общий знаменатель можно свернуть в разность квадратов. В итоге у нас получится:
2a + b = 2a2 - 2ab + ab + b2 =
a + b a - b a2 - b2 a2 - b2
= 2a2 - 2ab + ab + b2 = 2a2 - ab + b2
a2 - b2 a2 - b2
Пример 2. Выполните вычитание дробей:
b - 2
a2 - ab a - b
Решение: разложим знаменатель первой дроби на множители:
a2 - ab = a(a - b)
Так как данное выражение делится на знаменатель второй дроби, то возьмём его в качестве общего знаменателя. Значит, теперь нам надо умножить числитель второй дроби на дополнительный множитель a:
2 · a = 2a
Получаем:
b - 2 = b - 2a = b - 2a
a2 - ab a - b a(a - b) a(a - b) a(a - b)
Пример 3. Выполните сложение:
x + x2
1 - x
Решение: запишем первое слагаемое в виде дроби и приведём её к знаменателю 1 - x:
x + x2 = x + x2 = x(1 - x) + x2 = x - x2 + x2
1 - x 1 1 - x 1 - x 1 - x 1 - x 1 - x
Теперь можно выполнить сложение дробей с одинаковыми знаменателями:
x - x2 + x2 = x - x2 + x2 = x
1 - x 1 - x 1 - x 1 - x
Точно также можно выполнять сложение и вычитание алгебраических дробей с любыми многочленами.
Объяснение:
Пример №1 (б):
(в скобках приведем разность и вычитаемое к общему знаменателю)
(дробь за скобкой перевернем, заменив тем самым деление на умножение)
(раскроем скобки)
(в дроби за скобкой числитель свернем по формуле квадрата разности, а в знаменателе этой дроби вынесем общий множитель 4z^2 за скобку)
(приведём подобные в числителе первой дроби)
(сократим в знаменателе первой дроби (3z-2) и в числителе второй дроби (3z-2))
(в числителе первой дроби вынесем общий множитель -12z за скобку)
(сократим -12z в числителе первой дроби и 4z^2 в знаменателе второй дроби на 4z)
(сократим (z+1) в числителе первой дроби и (z+1) в знаменателе второй дроби)
(раскроем скобки в числителе и знаменателе дроби соответственно)
(раскроем скобки)
ответ: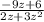
Пример №2 (в):
(в первой скобке приведем две дроби к общему знаменателю)
(во второй скобке приведем две дроби к общему знаменателю)
(раскроем скобки и приведем подобные в числителе первой дроби)
(приведем подобные в числителе второй дроби)
(вынесем общий множитель 3 в числителе первой дроби)
(сократим знаменатель первой дроби (u+3) и числитель второй дроби (u+3))
(сократим числитель первой дроби и знаменатель второй дроби на 3)
(сократим (u-3) в числителе первой дроби и (u-3) в знаменателе второй дроби)
ответ: 1