25 (км/ч)
Объяснение:
Расстояние против течения - Sпр.теч. = 100 км
Время против течения - tпр.теч. = 4часа
Расстояние по течению - Sпо теч. = 150 км
Время по течению - tпо теч. = 5 часов
На сколько км/ч скорость течения реки меньше собственной скорости лодки?
Пусть Vc. - собственная скорость лодки, а Vт. - скорость течения реки.
⇒ Vпо теч.=Vс. + Vт., Vпр.теч. = Vс. - Vт.
Чтобы найти скорость, нужно расстояние разделить на время:
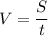
Найдем скорости по течению и против течения:
Vпр.теч. = 100:4 = 25 (км/ч)
Vпо теч. = 150:5 = 30 (км/ч)
Получим систему:
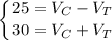
Сложим уравнения и найдем Vc.:
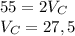
Собственная скорость лодки Vс.=27,5 км/ч
Найдем скорость течения реки:
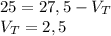 (км/ч)
(км/ч)
Найдем, на сколько км/ч скорость течения реки меньше собственной скорости лодки:
27,5 - 2,5 = 25 (км/ч)
Точки с координатами (-2;8) и (1;5)
Объяснение:
Первая функция
у= х²+4 (1)
Выразим у во второй функции:
х+у = 6 <=> у = 6-х (2)
Точка пересечения - точка, с некими координатами (х0;у0), которые принадлежат обоим графикам функций.
То есть нам надо найти такие х и у, для которых верно равенство 1 и 2.
Приравняем у в (1) и (2) функциях. Получим:
у = х²+4 = 6-х
Или
Найдем у для х=(-2) и х=1
Для этого подставим значение х в любую из 2х функций
При х = (-2)
у(-2) = 6-(-2) = 6+2 = 8
Следовательно одна из искомых точек имеет координаты:
(-2;8)
При х=1
у(1) = 6-1 = 5
Следовательно вьорая искомая точек имеет координаты:
(1;5)
ответ: (-2;8) и (1;5)