Для начала вспомним все три признака подобности треугольников:
I признак подобия треугольников - если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников - если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак подобия треугольников - если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
Задача 1
∠ABC = ∠DEF = 90°, ∠ACB = ∠DFE = 55°, значит за первым признаком подобности треугольников ΔABC ~ ΔDEF.
Задача 2
Катеты - это прямые (в прямоугольном треугольнике), которые образуют прямой угол. Гипотенуза - это прямая, которая соединяет два катета. Значит, CV и VN - катеты, а CN - гипотенуза.
Задача 3
В прямоугольном ΔABC катеты AB и BC (AB = 5.9 см, BC = 5 см) образуют угол 90°.
В прямоугольном ΔDEF катеты DE и EF (DE = 5.9 см, EF = 5 см) образуют угол 90°.
Сделаем пропорцию:
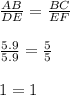
Значит эти треугольники подобные по второму признаку подобия треугольников
II признак подобия треугольников простыми словами - если одна сторона первого треугольника в k раз больше соответственной стороны второго, и вторая сторона первого треугольника тоже в k раз больше соответственной стороны второго, и эти две стороны в своих треугольниках создают углы, которые равны между собой, то эти треугольники подобны.
Если эти треугольники подобны, то все их углы равны между собой. Благодаря этому нам без разницы где находится меньшие углы: меньший угол ΔDEF будет находится там же, где и меньший угол ΔABC. Значит, меньший угол ΔDEF = меньшему углу ΔABC = 42°
ответ: 60 деталей. 30 деталей.
Объяснение:
Решение.
Пусть второй автомат в час изготавливает х деталей. Тогда
первый автомат изготавливает х+30 деталей.
Время на изготовление 180 деталей 1 автоматом равно 180/(х+30) часов
а время для 2 автомата равно 180/х часов.
Разница во времени равна 3 часа. Составим уравнение:
180/х - 180/(х+30) = 3;
180*(x+30) - 180x = 3x(x+30);
180x+ 5400 - 180x = 3x²+90x;
3x²+90x-5400=0; [: 3]
x²+30x-1800 = 0;
x1=30; x2= -60 - не соответствует условию
х=30 деталей изготавливает 2 автомат;
х+30 = 60 деталей изготавливает 1 автомат;
это алгебра. 16+11+12=39
45-39=4