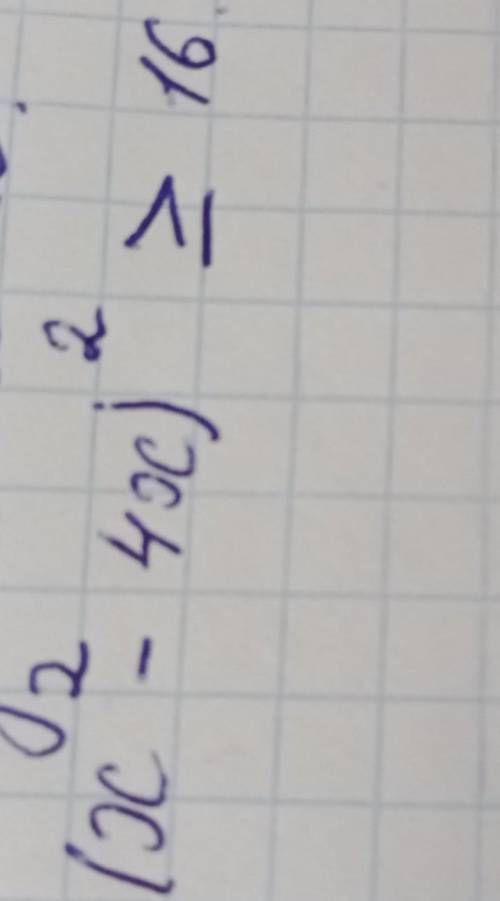
каноническое уравнение прямой имеет вид
(х-х₁)/l=(у-у₁)/m=(z-z₁)/n, где
{l; m; n}- направляющий вектор прямой.
(х-х₁)/(х₂-х₁)=(у-у₁)/(у₂-у₁)=(z-z₁)/(z₂-z₁)- уравнение прямой, проходящей через две точки (x₁; y₁; z₁) и (x₂; y₂;z₂). причем абсолютно все равно, какую точку Вы назовете (x₁; y₁; z₁) , а какую (x₂; y₂;z₂) . К примеру, у меня
х₂-х₁=4-2=2=l ; у₂-у₁=3-(-3)=6=m ; z₂-z₁=-10-6=-16=n .
каноническое уравнение прямой имеет вид
(х-2)/2=(у+3)/6=(z-6)/(-16),
параметрическое же уравнение получим, когда приравняем эти три равные отношения к параметру t
(х-2)/2=t⇒x=2t+2
(у+3)/6=t⇒y=6t-3
(z-6)/(-16)=t⇒z=-16t+6
1 неравенство - вся числ. прямая
2 неравенство - не имеет решений
3 неравенство - открытый промежуток
4 неравенство - объединение двух промеж
Объяснение:
ax²+bх+c ≥ 0
ах²+bх+с ≤ 0
D = b²-4ас
Если D<0, но при этом a>0 и само неравенство > 0 => его решение - вся числовая прямая
Если D<0, но при этом a<0, и само неравенство ≥ 0 => оно не имеет решений
Если D>0, но при этом a>0 и само неравенство < 0 => решение - открытый промежуток
Если D>0, но при этом а<0 и само неравенство <0 => решение - объединение двух промежутков
x принадлежит (-бесконечности; 2-2*2^(1/2)] U {2} U [2+2*2^(1/2); + бесконечность)
Объяснение:
(x^2-4*x)^2 - 16 >=0
(x^2 - 4*x)^2 - 4^2 >=0
(x^2-4*x - 4)*(x^2 - 4*x + 4)>=0
(x^2 - 4*x - 4) * (x - 2) ^ 2 >= 0
найдем корни x^2 - 4*x - 4 = 0
D = 16 + 16 = 32
x = (4 - 4*2^(1/2))/2
x = (4 + 4*2^(1/2))/2
2^(1/2) - корень из двух
нули функции
+++ --- +
2 - 2*2^(1/2) 2(корень четной степени) 2 + 2*2^(1/2)