Спростить виразив обчислить його значення: 2ab(3a²– 2²) – 3ab(ab² - a²), якщо

👇

Увидеть ответ

Открыть все ответы

Ответ:

zaycevakatyany

02.09.2022

(1;2) (2;1)

Объяснение:

Мы видим так называемую симметрическую систему уравнений(при замене переменных друг на друг, система не изменится. Для такой системы есть стандартная замена xy=t, x+y=k

, тогда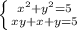 $\left \{ {{x^2+y^2=5} \atop {xy+x+y=5}} \right.$ перепишем как 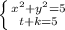$\left \{ {{x^2+y^2=5} \atop {t+k=5} \right.$ . Теперь нужно представить уравнение в первой строке системы через новые переменные, для этого попробуем выделить полный квадрат, x²+y² из этой суммы можно получить 2 вида квадрата, квадрат суммы и квадрат разности, нам выгодно сделать сумму, тогда добавим 2xy, но чтобы ничего не изменилось вычтем 2xy. Тогда (x²+2xy+y²)-2xy=5. Свернем (x+y)²-2xy=5. Теперь мы видим наши замены в чистом виде 1-ая строка = k²-2t=5.

$\left \{ {{k^2-2t=5} \atop {k+t=5}} \right.$ . Теперь перейдем к следующему. из второго уравнения вычтем t из обеих частей, тогда k=5-t. и подставим это значение k в первое.

$\left \{ {{((5-t)^2-2t=5} \atop {k=5-t}} \right.$ Расскроем скобки, t²-10t+25-2t-5=0

t²-12t+20=0. Получили квадратное уравнение, которое решаем любым удобным (для меня Т. обратная Т.Виета)

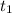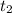t=10 или t=2. удобнее записать так $t_{1}$ =10 $t_{2}$ =2, отсюда найдем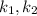 $k_{1},k_{2}$

$k_{1}$ =5- $t_{1}$ =5-10=-5, $k_{2}$ =5- $t_{2}$ =5-2=3.

Теперь обратные замены в 2 системы

$\left \{ {{xy=10} \atop {x+y=-5}} \right.$ . опять замена), x=-5-y., -5y-y²=10,y²+5y+10=0, D=25-40,эта система решений не имеет( на множестве действительных чисел)

$\left \{ {{xy=2} \atop {x+y=3}} \right.$ . Опять замена x=3-y. 3y-y²=2, y²-3y+2,тогда $y_{1}$ =2, $y_{2}$ =1. Тогда $x_{1}$ =1, $x_{2}$ =2. Что не удивительно, т.к. в симметрических системах достаточно получить ответ лишь для одной переменной и просто поменять местами с другой, но мы в этом, так сказать, убедились.

ответ 2 пары чисел (1;2) (2;1)

4,4(28 оценок)

Ответ:

melitatomashko

02.09.2022

Пусть расстояние между пунктами А и В будет S, пусть также, что скорость пассажирского поезда v_1 (км/ч), а скорость товарного поезда v_2 (км/ч). Тогда по условию задачи составим уравнения: S = v_1*4,

S = v_2*6, то есть

v_1*4 = v_2*6, это первое уравнение.

После того как поезда встретились, за два часа пассажирский поезд проехал v_1*2 км, а товарный v_2*2 км (в разных направлениях), поэтому расстояние между ними будет v_1*2 + v_2*2 = 320 км, это второе уравнение. Решаем систему из двух уравнений:

v_2 = v_1*4/6 = (2/3)*v_1,

подставляем это во второе уравнение системы

v_1*2 + (2/3)*v_1*2 = 320,

v_1*( 2+ (4/3) ) = 320

v_1*(10/3) = 320,

v_1 = 320*(3/10) = 32*3 = 96 (км/ч)

v_2 = (2/3)*96 = 2*32 = 64 (км/ч)

ответ. Скорость пассажирского поезда 96 км/ч, а скорость товарного поезда 64 (км/ч).

4,5(65 оценок)

Это интересно:

Мир-работы

11.09.2020