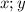 из набора множеств от -100 до 100 , то нужно найти
из набора множеств от -100 до 100 , то нужно найти 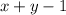 . Очевидно что если мы будет брать крайние числа , по закону перемещения ничего не изменится , можно даже решить ослабленную версию такой задачи где требуется найти сумму
. Очевидно что если мы будет брать крайние числа , по закону перемещения ничего не изменится , можно даже решить ослабленную версию такой задачи где требуется найти сумму 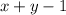 из множество чисел от 1 до 25 и.т.д .
из множество чисел от 1 до 25 и.т.д . 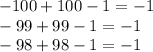 уже 100 операций проделано , теперь осталось 100
уже 100 операций проделано , теперь осталось 100 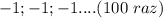
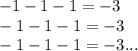 50 раз , следовательно 50 операций
50 раз , следовательно 50 операций
Если взять a=0, b=1, то получается элемент 1/2, квадрат которого равен 1/4 и поэтому не лежит в X. Таким образом, обычное умножение выводит из этого множества, и поэтому не имеет права претендовать на гордое название "алгебраической операции". После этого смешно говорить про ассоциативность (а она бы была, если бы операция не выводила бы из X), про коммутативность (а она бы... - см. текст выше), наличие нейтрального элемента (см. выше). Не знаю, какие элементы Вы называете симметричными, обычно говорят про обратные, но здесь с обратными проблема. В общем, говорить о группе не приходится, как и о группоиде, полугруппе или моноиде