1) x (-бесконечность;-6)V(-6;+бесконечность)
2) все числа
3) x (-бесконечность; -5)V(-5;+5)V(+5;+бесконечность)
4) x (-бесконечность; -5)V(-5;+5)V(+5;+бесконечность)
5) по идее не решается
Объяснение:
1) Нельзя, чтобы знаменатель делился на ноль, мы пишем: х+6>0 и переносим, меняя знак, тогда х>-6
2) подойдут любые числа
3) то же самое, что и в первом: x^2-25>0 x^2>25, корень 25 это пять, но т.к. квадрат, то + и -5.
4) аналогично третьему
5) не решается потому, что x^2+1>0 x^2>-1, корень из -1 не может быть, т.к. под корнем никогда не должно быть минуса
DenQ04a Ученый
б)
Строим таблицу, где первая колонка х, а вторая у.. .
ниже таблицы пишем
2х² + у = 4х - 3
2х² - 4х = -3 - у
При х=0, у=-3
х=1, у=-1
х=2, у=-3
х=3, у=-9
х=4, у=-19
(это пишем в таблицу)
Отмечаешь эти точки на координатной плоскости и соединяешь,
сначала имеет параболы, а от точки (2,-3) идет на низ прямая
в) xy = 8
y = 8/x
График - Гипербола
Строим таблицу
x≠0
x = -8, y = -1
x = -4, y = -2
x = -2, y = -4
x = -1, y = -8
x = 8, y = 1
x = 4, y = 2
x = 2, y = 4
x = 1, y = 8
Отмечаешь на координатной плоскости и проводишь Гиперболу.
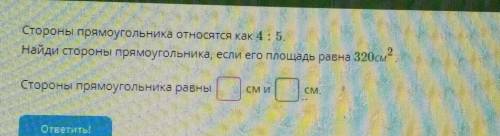
a = 16 см
b = 20 см
Объяснение:
S = ab
Раз в задаче указано, что стороны относятся как 4:5, то это значит, что сторона a равна 4x, сторона b - 5x:
S = 4x*5x = 320
20x² = 320
x² = 16
x = ±4 см
x = 4 (т.к. не существует отрицательных сторон)
a = 4x = 4*4 = 16 см
b = 5x = 5*4 = 20 см