24 см.
Объяснение:
Пусть один катет прямоугольного треугольника будет а см , а другой bсм.
Тогда площадь равна 0,5*а* b, а квадрат гипотенузы найдем по теореме Пифагора а² + b² . Так как по условию площадь равна 24 см², а гипотенуза равна 10 см , то составляем систему уравнений:
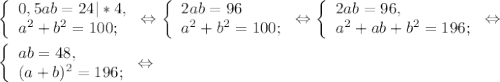

Так как a и b катеты прямоугольного треугольника , а значит положительные числа .Тогда их сумма не может быть отрицательным числом. Поэтому вторая система не подходит по смыслу задачи.
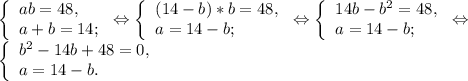
Решим квадратное уравнение:
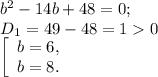
Если b=6, то а=8
Если b=8, то а=6
Значит катеты прямоугольного треугольника 6 см и 8 см. Тогда периметр ( сумма длин всех сторон треугольника)
P= 6+8+10 = 24 (см)
1) f(x)=7x-14, [0;4]
производная равна 7, 7≠0, , поэтому нет критических точек, и наибольшее и наименьшее свое значение функция принимает на концах отрезка.
f(0) = -14-наименьшее значение.
f(4) =14 наибольшее значение функции
2) f(x)= -0,2x + 0,4, [1;3]
аналогично 1) производная -0.2≠0, ищем значения функции на концах отрезка, т.е. f(1) =-0.2+0.4=0.2- наибольшее значение.
f(3) =-0.6+0.4=-0.2-наименьшее значение.
3) f(x)= 6/x, [1;6]
производная равна -6/х²≠0, не существует в точке 0, но эта точка не входит и в область определения. ищем значения функции на концах отрезка, т.е. f(1) =6/1=6- наибольшее значение.
f(6) =6/6=1- наименьшее значение.
4) f(x)= -5/x, [-5;-1]
Производная равна 5/х²≠0 не существует в точке 0, но эта точка не входит и в область определения. ищем значения функции на концах отрезка, т.е. f(-1) =-5/(-1)=5- наибольшее значение.
f(-5) =-5/(-5)=1- наименьшее значение.
ну вроде 60 с б и а б в г д е ё ж з к л м н о п р с т у и к л м н о п р
Объяснение:
ну если а это б тогда б это с с это д
воот воот