(-5; -8/5) ; (8; 1)
Объяснение:
{ x - 5y = 3
{ xy = 8
выразим x из первого уравнения системы
x - 5y = 3 ⇒ x = 3 + 5y
подставим полученное значение x во второе уравнение системы
(3 + 5y) * y = 8
3y + 5y² = 8
5y² + 3y - 8 = 0
D = 3² + 4 * 5 * 8 = 9 + 160 = 169
y = (-3 ± √169) / (2 * 5) = (-3 ± 13) / 10
y₁ = (-3 - 13) / 10 = - 16/10 = - 8/5
y₂ = (-3 + 13) / 10 = 10/10 = 1
подставим каждое из полученных значений y в уравнение x = 3 + 5y
x₁ = 3 + 5y₁ = 3 + 5 * (-8/5) = 3 - 8 = -5
x₂ = 3 + 5y₂ = 3 + 5 * 1 = 3 + 5 = 8
получили две пары чисел, являющихся решением заданной системы: (-5; -8/5) и (8; 1)
Общий вид квадратного уравнение следующее
a·x²+b·x+c=0, где a≠0.
Неполное квадратное уравнение имеет один из следующих видов:
a·x²+c=0 когда b=0; a·x²+b·x=0 когда c=0;a·x² = 0 когда b=c=0.1. a) Если неполное квадратное уравнение имеет вид a·x²+c=0 и c/a<0, то квадратное уравнение a·x²+c=0 имеет корни равные по модулю, но противоположные по знаку:
a·x²+c=0 ⇔ a·x² = -c ⇔ x² = -c/a, так как -c/a>0 ⇔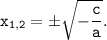
Тогда
Отсюда условие:
b=0 и c/a<0!
b) Если неполное квадратное уравнение имеет вид a·x²=0, то квадратное уравнение a·x²=0 имеет единственный корень:
a·x²=0 ⇔ x²=0 ⇔ x=0.
Отсюда условие:
b=c=0!
В случае a·x²+b·x=0 квадратное уравнение имеет два корня:
a·x²+b·x=0 ⇔ x·(a·x+b)=0 ⇒ x₁=0, x₂= -b/a.