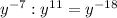Представьте выражение в виде степени с основанием a или произведения степеней с разными основаниями: 1) b^-7×b^15; 2) b^-10÷b^-16; 3) (m^6n-4p^8)^-5; 4) (m^9/n^-8)^6×(m^-10/n^26)^-2 5) x^-9×x^16; 6) y^-7÷y^-11.
Заметим, что для двух неравных натуральных чисел n < m наибольший общий делитель не превышает [m/2], где квадратные скобки означают округление вниз до ближайщего целого. Тогда среди всех чисел, меньших 100, наибольшие общие делители могут принимать значения от 1 до 49 — всего 49 вариантов. Так как синих чисел как раз 49, то каждое число от 1 до 49 написано по разу.
Простые числа 41, 43 и 47 должны быть написаны синим. Существует только один получить такие числа: надо написать рядом красные 41 и 82, 43 и 86, 47 и 94. Поскольку все остальные числа взаимно просты с 41, 43 и 47, то радом с красными 41, 43 и 47 будут написаны по синей единице, и синих единиц будет не меньше двух.
1)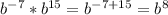
2)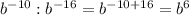
3)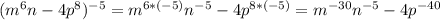
4)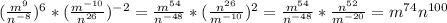
5)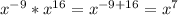
6)