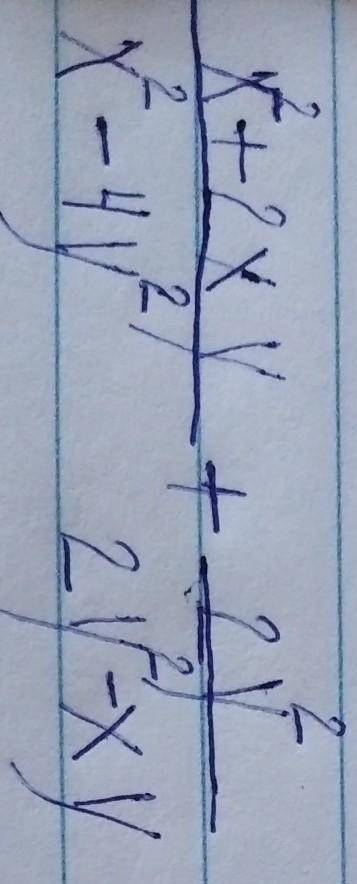
ну в место 51 поставь 52
Объяснение:
Обозначим:
а - длина прямоугольника;
в - ширина прямоугольника
Согласно условия задачи,
2*(а+в)=40
а*в=51
Решим получившуюся систему уравнений, для этого из второго уравнения найдём значение (а) и подставим её значение в первое уравнение:
а=51/в
2*(51/в+в)=40
(102+2в²)/в=80
102+2в²=40в
2в²-40в+102=0 сократим на 2
в²-20в+51=0
в1,2=(20+-D/2*1
D=√(20²-4*1*51)=√(400-204)=√196=14
в1,2=(20+-14)/2
в1=(20+14)/2
в1=17 - не соответствует условию, т.к. для ширины большая величина
в2=(20-14)/2
в2=3 (см - ширина прямоугольника)
а=51/3
а=17 (см - длина прямоугольника)
ответ: в прямоугольнике длина - 17см; ширина 3см
По теореме косинусов
64*3 = r^2 + r^2 - 2* r^2 * cos 120
192 =2 * r^2 + 2 * r^2* cos 60
192 =2 * r^2 + 2 * r^2* 1/2
192 = 3* r^2
r^2 = 64 см
r = 8 см
Из треугольника АОС, т к. угол осевого сечения при вершине С равен 90 градусов
угол САО = угол ОСА = 45 гр. , следовательно СО =ОА = 8 см
Из треугольника ОВК:
ОК = (64 — 16*3)^(1/2) = 4
Из треугольника КОС
КС = (СО^2 + OR^2)^(1/2) = (64 +16)^(1/2) = 4*(5)^(1/2)
Итак, искомая площадь
S = 1/2*AB*CK = 1/2 * 8*(3)^(1/2)*4*(5)^(1/2) = 16*(15)^(1/2) cм^2
ответ: S = 16*(15)^(1/2) cм^2
1
Объяснение:
Все х и у сокращаются, фото ниже