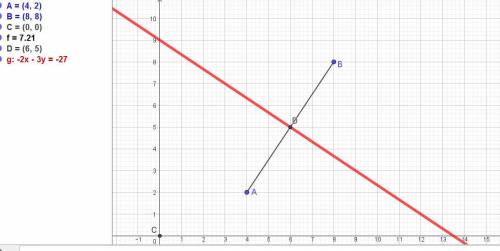
Прямая,все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это перпендикуляр к середине отрезка АВ.
Уравнение АВ: (х - 4)/(8 - 4) =(у - 2)/(8 - 2).
(х - 4)/4 =(у - 2)/6) или (х - 4)/2 =(у - 2)/3.
Или в общем виде Ах + Ву + С = 0.
3х - 12 = 2у - 8,
3х - 2у - 4 = 0. Здесь А = 3, В = -2.
Перпендикулярная прямая имеет вид -Вх + Ау + С1 = 0.
Для определения коэффициента С1 надо подставить координаты точки, принадлежащей этой прямой.
Такая точка - середина АВ (точка Д).
Д = (1/2)(A(4;2) + B(8;8))/2 = (6; 5). Подставляем:
2*6 + 3*5 + С1 = 0,
С1 = -12 - 15 = -27.
ответ: уравнение прямой, все точки которой находятся на равных расстояниях от точек A(4;2) и B(8;8), это 2х + 3у - 27 = 0.
х ( км/ч ) - скорость первого поезда.
y ( км/ч ) - скорость второго поезда.
10х ( км ) - расстояние, которое проедет первый поезд за 10 ч.
10y ( км ) - расстояние, которое проедет второй поезд за 10 ч.
10х+10y ( км ) - расстояние между городами, которое по условию задачи равно 650 км.
Получаем первое уравнение: 10х+10у=650
8 ч + 4 ч 20 мин = 12 ч 20 мин
12 ч 20 мин =12 20\60ч=740\60ч
740\60х(км) расстояние которое проедет первый поезд за 12 ч 20 мин
8y ( км ) - расстояние, которое проедет второй поезд за 8 ч.
740\60 х + 8y ( км ) - расстояние между городами, которое по условию задачи равно 650 км.
Получаем второе уравнение: 740\60х+8у=650
получаем систему:(см.влож)
ответ: первый поезд проходит 30 км/ч, второй 35 км/ч.

Объяснение:
15а³-(14a+3a³-(a³-6a)) = 15а³ - 14a - 3a³ + (a³-6a) = 12a³ - 14a + a³ - 6a = 13a³ + 8a