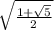
7x²=21x
Перенести условия в левую часть
72=21
72−21=0
Простой фактор
72=21
7(2−3)=0
Разделите обе части уравнения на один и тот же член
7(2−3)=0
2−3=0
Используйте формулу корней квадратного уравнения
=−±2−4/√2
Приведите уравнение к общему виду, определите коэффициенты a, b и c, затем вставьте их в формулу.
2−3=0
=1
b=-3
=0
=−(−3)±√(−3)2−4⋅1⋅0/2⋅1
Упростите
Возведите в степень
Умножьте на ноль
Сложите числа
Вычислите квадратный корень
Умножьте числа
x=3±3/2
Разделите уравнение
Чтобы найти неизвестное, разложите уравнение на два: одно – с плюсом, другое – с минусом.
=3+3/2
=3−3/2
Найдите значения
Чтобы решить уравнение, преобразуйте его и вычислите неизвестное.
=3
=0
9x²=27x
Перенести условия в левую часть
92=27
9x^{2}=27x9x2=27x
92−27=0
Простой фактор
92−27=0
9x^{2}-27x=09x2−27x=0
9(2−3)=0
9(x^{2}-3x)=09(x2−3x)=0
Разделите обе части уравнения на один и тот же член
9(2−3)=0
9(x^{2}-3x)=09(x2−3x)=0
2−3=0
Используйте формулу корней квадратного уравнения
=−±2−4/√2
Приведите уравнение к общему виду, определите коэффициенты a, b и c, затем вставьте их в формулу.
²−3=0
=1
=−3
=0
=−(−3)±√(−3)²−4⋅1⋅0/2⋅1
Упростите
Возведите в степень
Умножьте на ноль
Сложите числа
Вычислите квадратный корень
Умножьте числа
=3±3/2
Разделите уравнение
Чтобы найти неизвестное, разложите уравнение на два: одно – с плюсом, другое – с минусом.
=3+3/2
=3−3/2
Найдите значения
Чтобы решить уравнение, преобразуйте его и вычислите неизвестное.
=3
=0
Решение системы уравнений (1; -3).
Объяснение:
Решите методом сложения систему уравнений:
7x-y=10
5x+y=2
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе ничего преобразовывать не нужно, коэффициенты при у одинаковые и с противоположными знаками.
Складываем уравнения:
7х+5х-у+у=10+2
12х=12
х=1
Подставим значение х в любое из двух уравнений системы и вычислим у:
7x-y=10
-у=10-7х
у=7х-10
у=7*1-10
у= -3
Решение системы уравнений (1; -3)