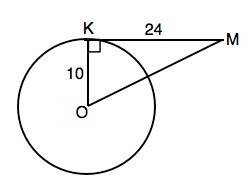
Обозначим центр окружности О, точку касания К.
Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∆ МОК - прямоугольный.
Отношение катетов 10:24=5:12 указывает на то, что длины сторон треугольника из Пифагоровых троек 5:12:13, в которых эти длины –целые числа.⇒ МО=2•13=26. И это можно проверить по т.Пифагора.
МО=√(KO²+KM²)=√676=26
В прямоугольном треугольнике каждый катет является высотой, проведенной к другому катету.
Площадь прямоугольного треугольника равна половине произведения катетов:
S=КМ•КО:2=24•10:2=120 см²
В решении.
Объяснение:
а) 0,6х²у * ? = -3х⁴у
? = - 3х⁴у / 0,6х²у =
3 и 0,6 сократить (разделить) на 0,6; х⁴ и х² на х²; у и у на у:
= - 5х²;
б) ? * (-4ху²) = 8,2х³у³
? = 8,2х³у³ / (-4ху²)=
сократить (разделить) 8,2 и 4 на 4; х³ и х на х; у³ и у² на у²:
= -2,05х²у;
в) -5ху * ? = 0,8х²у³
? = 0,8х²у³ / (-5ху)=
сократить (разделить) 0,8 и 5 на 5; х² и х на х; у³ и у на у:
= -0,16ху².
Проверка путём подстановки вычисленных значений неизвестной величины в выражения показала, что данные решения удовлетворяют данным выражениям.
/ - знак деления.