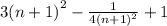последовательность является строго монотонной возрастающей, но не имеет предела, так что это доказать невозможно. Строго монотонна она потому что при неограниченном возрастании n первое слагаемое в рекурентной формуле неограниченно возрастает, а второе слагаемое постоянно убывает, в то время как 3е остается неизменным. То есть на каждом новом шаге мы все из большего вычитаем все меньшее. А предела не имеет так как послеовательноть не является ограниченной, это раз, и не выполняется критерий коши для сходимости последовательности, т.е. она не является фундаментальной, это 2
Пусть его скорость была -хкм/ч. первый за 2 часа проехал 16*2=32 км, что бы его догнать нужно 32/(х-16) часов. второй за 1 час проехал 10 км, что бы догнать второго нужно 10/(х-10) часов. разница в гонке между ними известно по условию. состовляем уравнение 32/(х-16)-10/(х-10)=4,5 32х-320-10х+160=4,5(х-10)(х-16) при х≠10 и х≠16 22х-160=4,5(х²-26х+160) 4,5х²-139х+880=0 д=59² х1=(139+59)/9=22 х2=(139-59)/9=8.(8) так как х2< 10 то это не может быть решением, так как он никогда не догнал бы даже второго велосипедиста. получаем ответ при х=22км/ч ответ: 22 км/ч
x2=3*2^2-1/4*2^2+1=12-1/16+1=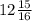
x100=3*100^2-1/4*100^2+1=30000+1-1/40000=30000\frac{39999}{40000}
последовательность является строго монотонной возрастающей, но не имеет предела, так что это доказать невозможно. Строго монотонна она потому что при неограниченном возрастании n первое слагаемое в рекурентной формуле неограниченно возрастает, а второе слагаемое постоянно убывает, в то время как 3е остается неизменным. То есть на каждом новом шаге мы все из большего вычитаем все меньшее. А предела не имеет так как послеовательноть не является ограниченной, это раз, и не выполняется критерий коши для сходимости последовательности, т.е. она не является фундаментальной, это 2
Забыл: Xn+1=