Объяснение:
y = 30x + 12
С Оy: х=0
y(0)=12
(0; 12) - точка пересечения с Oy
C Ох: y=0
30х + 12 = 0
х = -12 : 30
х = -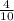 
х = -0,4
(-0,4; 0) - точка пересечения Ох
.
.
.
. Но 
фактически лишнее неравенство, оно выполняется автоматически потому, что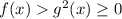 
, ибо полный квадрат всегда неотрицателен.
1. Из условия задачи - курицы у нас все разные. То есть если у нас мы возьмем какой-то набор птиц, в котором есть курица; и заменим эту курицу на другую, то получится другой набор
В таком понимании задачи, всего различных комбинаций птиц - 512 (учитывая комбинацию без птиц вовсе, каждую птицу можно взять или не взять, птиц всего 9, 2^9 вариантов). Воспользуемся кругами Эйлера к этой задаче: пусть круги означают кол-во комбинаций БЕЗ указанных птиц
БЕЗ гусей у нас 2^7 = 128 вариантов
БЕЗ кур - 64, а БЕЗ уток - 32 варианта
Далее, найдем кол-во комбинаций без гусей и без уток, без гусей и без кур, без кур и без уток. Без всех птиц у нас 1 единственная комбинация. Используя это, найдем кол-во вариантов для каждого из подмножества. Далее, вычтем из 512 все эти подмножества. Получим количество вариантов, где точно есть и утки, и гуси, и куры
ответ: 315
Пересечение С OX: (-0,4; 0) .
Пересечение С OY: (0; 12).
Объяснение:
1) График функции y = 30x + 12 пересекает ось OX в точке (x; 0), т.е. при условии y = 0
30x + 12 = 0 ; 30x =-12; x = -12/30 = -0,4
Точка пересечения оси OX (-0,4; 0)
2) График функции y = 30x + 12 пересекает ось OY в точке (0; y), т.е. при условии x = 0
y = 30*0 + 12 ; y = 12
Точка пересечения оси OY (0; 12)