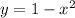
Это парабола, ветви которой направленны вниз, о чём говорит множитель -1 у 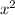 .
.
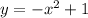
1 в данном случае обозначает, что график функции сдвинут вдоль оси Oy вверх на 1.
Т.е. отсюда видно, что функция, начинается выше оси Ох (принимая положительные значения) и в двух точках её пересекает своими ветвями, принимая отрицательные значения в дальнейшем. (Очевидно, что парабола может иметь не более двух точек пересечения с осью Ox, так что искать иных положительных значений не стоит)
Т.е. все множество положительных значений заключено между двумя корнями этой функции, а всё множество отрицательных, вне.
Корни видно из графика, это x_1 = 1 и x_2 = -1.
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
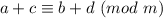
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
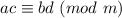
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
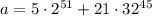
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, 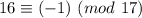 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что 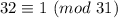 , получаем
, получаем
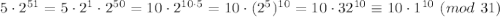
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
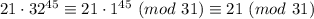
Остаток 21, чудесно. Выполняем последний шаг.
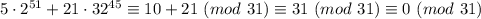
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
y=1-x2
у=-3 х=2
у=-8 х=3
у=-15 х=4
у=-3 х=-2
у=-8 х=-3 здесь функция принимает отрицатеоьне значения
у=1 х=0 функция принимает положительные значения