Объяснение:
Увеличивая знаменатель - мы уменьшаем дробь!
В данном случае знаменатель увеличился больше числителя, поэтому дробь вполне может уменьшится.
Пример:
5/6 и 8/10
8/10 = 4/5 < 5/6, так как первой не хватает до 1 1/5, а второй - 1/6,а 1/5 > 1/6
Но может и увеличится:
1/2 и 4/6
4/6 = 2/3 > 1/2
Можу я бути трохи нахабною і просити позначити мою відповідь кращою за повне пояснення і саму відповідь в сумі теж?
Відповідь:
1. ac+5a-bc-5b= (ac-bc)+(5a-5b) = c(a-b)+5(a-b) = (c+5)(a-b)
2. ac-5a+bc-5b = (ac+bc)-(5a+5b)[мінус по просту винесли за дужки так як там -5а-5б, то якби для того щоб було зручніше]=c(a+b)-5(a+b)=(c-5)(a+b)
3. ac+5a+bc+5b=(ac+bc)+(5a+5b)=c(a+b)+5(a+b)=(c+5)(a+b)
Пояснення:
ac+5a-bc-5b=
Згрупуємо
=(ac-bc)+(5a-5b) =
Винесемо спільний множник
=c(a-b)+5(a-b) =
Винесемо спільний множник
=(c+5)(a-b)
Інші приклади виконуються за тим самим прикладом, отож не бачу сенсу писать декілька разів одне й те саме
4) ΔCOД: ∠СОД=90° , ОВ - биссектриса ∠МОД ⇒ ∠ДОВ=∠ВОМ=20° ,
∠ДОМ=2*∠ДОВ=2*20°=40°
∠СОМ=∠СОД-∠ДОМ=90°-40°=50°
ОА - биссектриса ∠СОМ ⇒ ∠МОА=∠АОС=50°:2=25°
∠АОВ=∠МОА+∠ВОМ=25°+20°=45°
5) АД - высота ΔАВС ⇒ ∠АДС=90° ,
∠ДСА=32° , ∠ДСА=90°-∠ДСА=90°-32°=58°
∠ВАС=∠ВАД+∠ДСА=50°+58°=108°
∠АВС=180°-108°-32°=40°
6) ΔАВС , АД - медиана ⇒ ВД=ДС , АВ=15 см , АВ<АС ⇒ Р(ΔАВД)=38 см , Р(ΔАСД)=44 см
Обозначим а=ВД=ДС и m=АД
Р(АВД)=15+а+m=38 ⇒ a+m=38-15 , a+m=23
Р(ВАД)=а+m+AC =44 ⇒ 23+AC=44 , AC=44-23 , AC=21 (cм)
дана дробь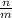
после преобразования получим дробь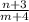
И получим
Таким образом, данное свойство верно для любой дроби