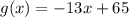 . Найдем значение
. Найдем значение  , при котором функция будет равна
, при котором функция будет равна 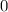 . Для этого приравняем саму функцию к
. Для этого приравняем саму функцию к 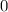 :
: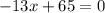
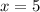 .
.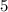 данная функция перескает ось абсцисс (OX). Так как у функции угловой коэффициент отрицательный (число -13), следует заключение, что функция убывает на всей области определения. Так как это линейная функция, то область определения у неё, вся числовая прямая. Отсюда следует, что функия - убывающая!
данная функция перескает ось абсцисс (OX). Так как у функции угловой коэффициент отрицательный (число -13), следует заключение, что функция убывает на всей области определения. Так как это линейная функция, то область определения у неё, вся числовая прямая. Отсюда следует, что функия - убывающая!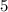 . Так как функция убывает, то отсюда получаем:
. Так как функция убывает, то отсюда получаем: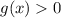 при
при 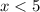
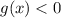 при
при  .
.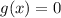 при
при 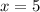
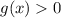 при
при 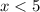
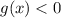 при
при 
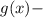 убывающая
убывающая
дано: треугольник KMN, AK=BN, AM=BM, CA перпендикулярно KM, CB перпендикулярно NM
доказать: MC - медиана треугольника KMN
В треугольнике KMN боковые стороны состоят из равных отрезков
AK=BN, AM=BM, следовательно
КМ=МК+АМ=ВN+MB=MN
Треугольник KMN - равнобедренный.
Δ КАС=Δ СВN,
так как это прямоугольные треугольники,
углы К и N равны как углы при основании равнобедренного треугольника,
катеты КА=ВN.
Если в прямоугольном треугольнике острый угол и катет равен острому углу и катету другого прямоугольного треугольника, то эти треугольники равны.
Следовательно, гипотенузы АС и CN этих треугольников равны.
АС=СN
Точка С - середина стороны КN
МС - медиана треугольника KMN, что и требовалось доказать.
Так как графиком функции «y = kx + b» является прямая линия, функцию называют линейной функцией. Из геометрии вспомним аксиому (утверждение, которое не требует доказательств), что через любые две точки можно провести прямую и притом только одну. ... Как проверить, проходит ли график через точку. Рассмотрим другое задание. Не выполняя построения графика функции «y = 2x