
х€(0; +оо)
Графическое решение
неравенств.
Объяснение:
Шаг 1.
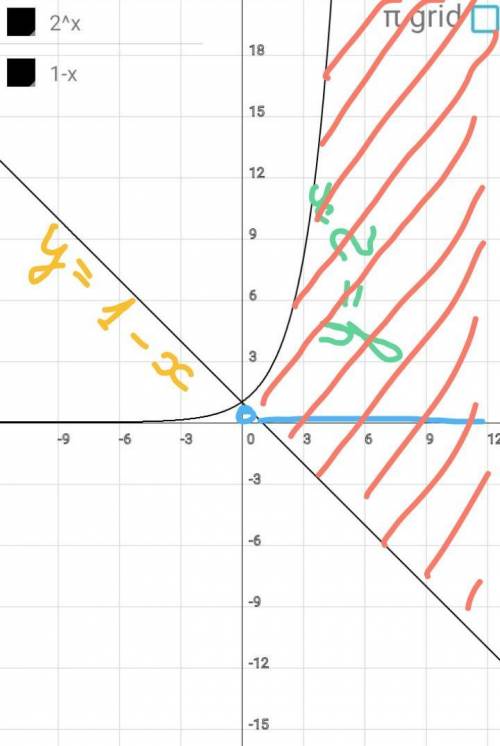
Строим график функции
у=2^х.
Показательная функция
а>1 ==> функция возрастает.
Пересекает ось ординат в
точке х=0.
у(0)=2^0=1
Шаг 2.
Строим график фцнкции
у=1-х или у=-х+1.
Линейная функция k<0
==> функция убывает.
Пересекает ось ординат в
точке х=0.
у(0)=0+1=1
Шаг 3.
В одной системе координат
строим графики функций
(по точкам).
Графики пересекаются в
точке (0; 1).
Шаг4.
Графически решаем задан
ное неравенство:
определяем участки, на кото
рых график функции у=2^х
расположен выше графика
функции у=-х+1.
х€(0; +оо).
х€(0; +оо)
Объяснение:
Система линейных уравнений может иметь:
одно решение, когда графики прямых пересекаются;
ни одного, когда графики параллельны;
бесконечное множество, когда графики сливаются (совпадают).
3)Сколько решений имеет система уравнений у = 2 х+1 и y=7 - 2x ?
Одно решение, прямые пересекаются, координаты точки пересечения (1,5; 4)
4) Сколько решений имеет система уравнений х - у = 5 и 3y - 3x = 4 ?
Ни одного, графики параллельны.
5) Сколько решений имеет система уравнений x-y= 5 и 3y - 3x = -15 ?
Бесконечное множество, графики сливаются (совпадают).