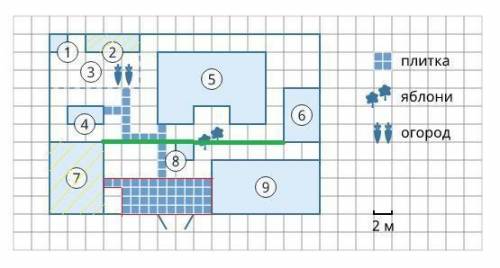
1) 5коробок 2) 60 м² 3) 20 м
Объяснение:
1) По рисунку видно, что 1 плитка 0,5*0,5 клетки, или с учетом масштаба:
0,5*0,5*2*2=1 м²
По схеме видно, что дорожка занимает 5*2 клеток и еще 0,5*1 клетку. Рассчитаем площадь плитки с учетом масштаба:
5*2*2*2+0,5*1*2*2=42 м² занимает площадь плитки от коровника к курятнику
42:1=42 плитки
42:10=4,2 коробки округляем в большую сторону до целого 5 коробок
2) Размер теплицы в клетках: 3*1
Размер коровника в клетках: 3*4
Площадь коровника и теплицы с учетом масштаба:
3*1*2*2+3*4*2*2=60 м²
3) Расстояние между двумя ближайшими точками - это расстояние от правого верхнего угла коровника до левого нижнего угла коровника.
Это 10 клеток или 10*2=20 м
1) 5коробок 2) 60 м² 3) 20 м
Объяснение:
1) По рисунку видно, что 1 плитка 0,5*0,5 клетки, или с учетом масштаба:
0,5*0,5*2*2=1 м²
По схеме видно, что дорожка занимает 5*2 клеток и еще 0,5*1 клетку. Рассчитаем площадь плитки с учетом масштаба:
5*2*2*2+0,5*1*2*2=42 м² занимает площадь плитки от коровника к курятнику
42:1=42 плитки
42:10=4,2 коробки округляем в большую сторону до целого 5 коробок
2) Размер теплицы в клетках: 3*1
Размер коровника в клетках: 3*4
Площадь коровника и теплицы с учетом масштаба:
3*1*2*2+3*4*2*2=60 м²
3) Расстояние между двумя ближайшими точками - это расстояние от правого верхнего угла коровника до левого нижнего угла коровника.
Это 10 клеток или 10*2=20 м

Формула суммы: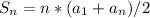
Формула n-го члена прогрессии: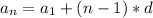
1) Подставим значения в формулы и выразим n:
| *n
2) Решим полученное квадратное уравнение:
Так как n не может быть дробным, n = 8
3) Найдём a_1:
4) Проверим сумму: