1. |x²-7|+12=0
|x²-7|=-12
x∈∅
Данное уравнение не имеет корней, т.к. модуль является неотрицательным числом.
2. Выделим полный квадрат:
x²-6x+8 = (x²-2x*3+3²) -3²+ 8 = (x-3)² -9 + 8 = (x-3)² -1
Разложим на множители x²-6x+8 = (x-x₁)(x-x₂)
По теореме Виета находим корни: х₁*х₂=8 и х₁+х₂=-6 => х₁=2 и х₂=4
x²-6x+8= (x-2)(x-4)
3. 3x²-6x+c=0, x₁=x₂
По условию, квадратное уравнение имеет равные корни, следовательно, дискриминант этого уравнения равен нулю.
Находим с:
D= (-6)²-4*3*c = 36-12c
36-12c = 0
12c = 36
c = 3
а).
Просто подставляем в уравнение, задающее функцию,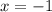 
:
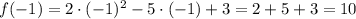
б).
Найдем те значения 
, при которых значение функции становится равным 
:
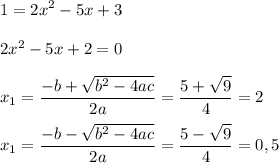
в).
Для того, чтобы определить, принадлежит ли точка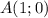 
графику, подставим в уравнение функци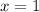и 
и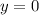 
, и посмотрим, что получится:
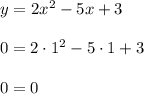
Получилось верное равенство! Значит, точка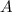 
действительно принадлежит графику рассматриваемой функции.
___________________________________________
Задание № 2.а).
Задача заключается в решении неравенства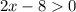 
:
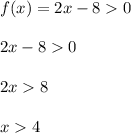
Получаем, что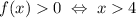 
, или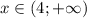 
.
б).
Ноли функции - это те значения , при которых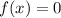 
:
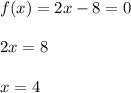
Значит, единственный ноль функции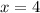 
.
___________________________________________
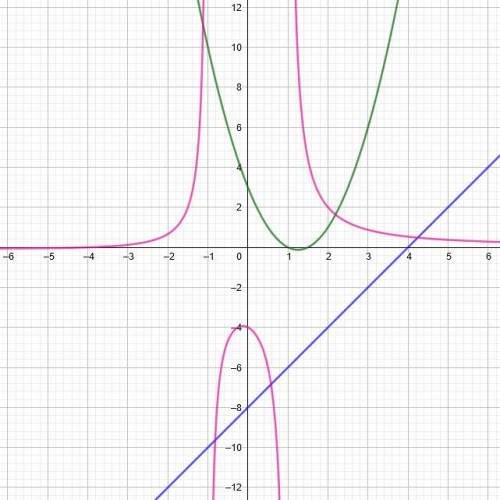
Задание № 3.а).
Область определения функции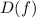 
- это те значения , при которых функция существует.
А функция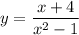 
существует только в том случае, если ее знаменатель не равен нолю:
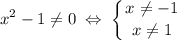
То есть, область определения данной функции - все действительные , кроме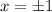 
:
Задача решена!
а) t^2+2tm+m^2
б) t^2-6t+9
в) 4t^2+4t+1
г) 9m^2-12mt+4t^2
д) 9m^4+6tm^2+t^2