2) Для каждого из уравнений подобрать корень из данных чисел: а) 2х+4=6 б) х-4=0 в) (х+1)(4+х)=0 г) 2(х-1)=х+4
Числа: 6; 2; 1; -1; -2; -4
3)Составьте уравнение, корнем которого является число 8
4) Выберите правильный ответ.
Уравнение х+5=5:
имеет множество корней;не имеет корней;имеет только один корень. Уравнение х+3=х:
а) имеет множество корней;
б) не имеет корней;
в) имеет только один корень 5) Найдите числа, которые нужно записать в квадратики, чтобы получилось верное равенство. 5 + □ = 13,5 - □=13,5 * □ = 15,13 = □ - 5,20 : □ = 5,5 = □ : 20,3 * □ – 5 = 10,15 – 2 * □ = 5,II. Восприятие и осознание нового материала. Рассмотрим два уравнения: х+5=7 и х-1=1 .Решением каждого из этих уравнений есть число 2 (х=2).Такие уравнения называются равносильными. Два уравнения называются равносильными, если они имеют одинаковые решения. Равносильными считаются и уравнения, не имеющие корней, например х+5=х и х-8=х. Вопрос классу : являются ли равносильными уравнения: а) х – 3= 0 и 3х =9; б) 0х = 3 и х+6=х? Какие из уравнений равносильны уравнению 3х=15: а) 6х=30; б)9х=45; в)3х-15=0; г)3х-1=14; д)3х+15=20; е)3х+15=18?
Чтобы решать более сложные уравнения, следует научиться заменять их более простыми уравнениями и равносильными данным.
Например, используя распределительное свойство умножения а(в+с)=ав+ас, можно утверждать, что значения выражений 5х+3х и 8х при любом значении х равны. Следовательно, равносильны такие уравнения: 5х+3х=10 и 8х=10.Другимим словами, если раскрыть скобки и привести подобные слагаемые в любой части уравнения, то получим уравнение равносильное данному.
Кроме того, если к обеим частям верного равенства прибавить одно и тоже число, то получится верное равенство. Например, если к обеим частям уравнения 3х=12-2х прибавить 2х, то получим уравнение 3х+2х=12 равносильное данному. Это все равно, что перенести члены уравнения из одной части в другую, при этом изменивши знак.
Мы также знаем, что если обе части числового равенства умножить или разделить на одно и тоже, отличное от нуля, число, то получим верное равенство. Поэтому, если обе части уравнения умножить или разделить на одно и то же , отличное от нуля, число, то получим уравнение равносильное данному.
Например, -3х+7=5, умножим обе части на (-1), получим 3х-7=-5. Эти уравнения имеют одни и те же корни.
Таким образом, всегда справедливы такие свойства уравнений.
Основные свойства уравнений :
1. В любой части уравнения можно привести подобныеслагаемые или раскрыть скобки, если они есть.
2.Любой член уравнения можно переносить из одной части уравнения в другую, изменивши его знак на противоположный. 3.Обе части уравнения можно умножать и делить на одно и то же число, отличное от нуля. Рассмотреть решение следующих уравнений с объяснением учителя: 3(х-1)=12; 2х-3=3х+2; . III. Закрепление и осознание знаний учащихся
1)Являются ли равносильными уравнения: а) 2х+5=10 и 2х=10; б)6-х=5 и х=11; 6х-1=2х+3 и 4х=4(ответ объяснить)
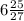
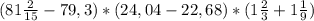
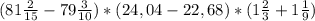
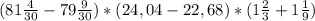
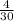
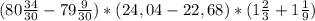
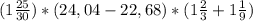
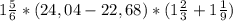
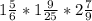
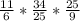
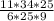
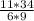
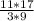
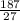
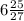
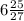
-5,82+(-7,18)-(-16,5)=-5,82-7,18+16,5=-1,36+16,5=-13+16,5=3,5
1/8-(-1/2)-4 5/8=1/8+4/8-4 5/8=5/8-4 5/8=-4
-2,49+2,67+(-3,18)=-2,49+2,67-3,18=0,18-3,18=-3
с-d-b
-5 3/8-5/9-(-11,1)=-43/8-5/9+11 1/10=-43/8-5/9+111/10=
-1935/360-200/360+3996/360=1861/369=5 61/360
Объяснение:
-на+=-
-на-=+
1)
два отрицательных числа складываем и ставим знак минус
-5,82-7,18=-(5,82+7,18)=-13
от большего отнимаем меньшее и ставим знак большего числа
16,5-13=3,5
2) -на-=+
приводим к общему знаменателю.
5/8-4 5/8=-4 от большего отнимаем меньшее и ставим знак большего числа.
3) от большего отнимаем меньшее и ставим знак большего числа
-2,49+2,67=0,18
2,67-2,49=0,18
0,18-3,18=-3
3,18-0,18=3, ставим знак большего числа =-3