А8.
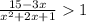
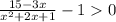
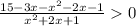
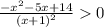ОДЗ: 
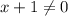
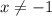
Так как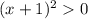 
, то
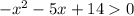
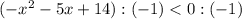
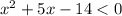
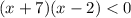
_____________-7////////////////////////////////2________________________
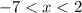
-6; -5; -4; -3; -2; -1; 0; 1 - целые из этого промежутка
Исключаем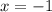 
по ОДЗ и находим сумму:
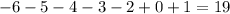
ответ: 19
А9.
Пусть 
- длина основания;
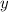- ширина основания;
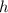- высота параллелепипеда, тогда по т. Пифагора выразим диагонали каждой грани через стороны:
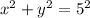
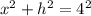
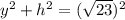
1) Сложим эти уравнения:
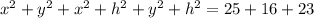
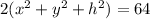
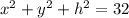
2) 
=> 
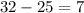
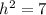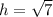
3) 
=> 
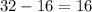
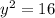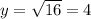
4) 
=> 
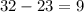
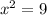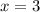
5) 
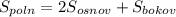
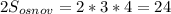
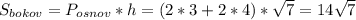
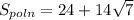
ответ: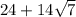 
х²-6х+9=-х²+2х+3
2х²-8х+6=0
D=64-48=16
x₁=(8+4)/4=3
x₂=(8-4)/4=1 получили пределы интегрирования
₃
S=∫₁ ((-x²+2x+3)-(x²-6x+9))dx= (-x²+2x+3-x²+6x-9)dx=(-2x²+8x-6)dx=
-2x³ 8x² ³ 2x³ ³ 2*3³ 2*1³
= + - 6x |= - + 4x²-6x | = - +4*3²-6*3 -( +4*1²-6*1)=
3 2 ₁ 3 ₁ 3 3
= -18+36-18-((-2/3)+4-6)=-((-2/3)-2)=-(-8*3)=8/3≈2,67