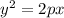 ее фокус находится в точке с координатами
ее фокус находится в точке с координатами 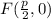
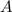 находиться в системе уравнения
находиться в системе уравнения 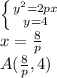 Если уравнение касательной равна
Если уравнение касательной равна 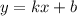 с учетом того что она проходит через точку
с учетом того что она проходит через точку 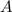 получаем
получаем 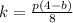 , подставляя
, подставляя 
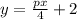
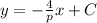 он проходит через точку
он проходит через точку 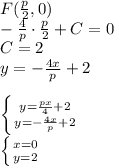
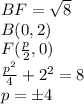
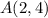
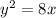
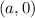 центр окружности (так как центр лежит на оси
центр окружности (так как центр лежит на оси 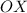 )
) 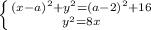
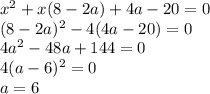
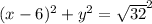
Как известно, объем шара вычисляется по формуле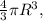 где R - радиус шара. Приравниваем суммарный объем n маленьких шаров и объем получившегося большого шара:
где R - радиус шара. Приравниваем суммарный объем n маленьких шаров и объем получившегося большого шара:
Поскольку по условию n=8; r=0,5, получаем![R=0,5\sqrt[3]{8}=0,5\cdot 2=1](/tpl/images/0149/3480/6fb23.png)
ответ: R=1 см