Выполни x2 - 3x + 2 = 0 x2 - 4x + 3 = 0
x2 - 5x + 4 = 0
x2 - 6x + 5 = 0
x2 - 7x + 6 = 0
x2 - 5x + 6 = 0 x2 + 3x + 2 = 0
x2 + 4x + 3 = 0
x2 + 5x + 4 = 0
x2 + 6x + 5 = 0
x2 + 10x + 9 = 0
x2 + 16x + 15 = 0
Найти сумму и разность корней
Найди корни уравнений по теореме, обратной теореме Виета
x2 - 9x + 8 = 0 x2 + 17x + 16 = 0
x2 - 6x + 8 = 0 x2 + 10x + 16 = 0
x2 - 11x + 10 = 0 x2 + 19x + 18 = 0
x2 - 7x + 10 = 0 x2 + 11x + 18 = 0
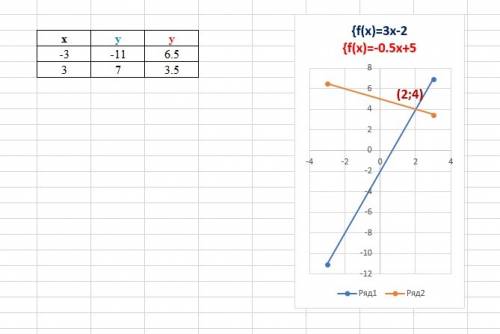
Это 2 прямые, первая с наклоном У:Х=0,5:1 сдвинута по оси У на 0,5 вниз (при Х=0 У=-0,5), а вторая с наклоном У:Х=1:1 сдвинута по оси У на 4 вниз (при Х=0 У=-4).
Точка пересечения имеет координаты (7;3), значит, корнем является Х=7.
2) Приводим систему к виду У=-1/3Х+2 и У=-1/3Х+3.
Это 2 прямые, первая с наклоном У:Х=1/3:1 сдвинута по оси У на 2 вверх (при Х=0 У=2), а вторая с наклоном У:Х=1/3:1 сдвинута по оси У на 3 вверх (при Х=0 У=3).
Имеем 2 параллельные прямые (наклон ведь одинаков), которые не пересекаются -> у системы нет решения.