
Сторона данного треугольника а(3) равна Р:3=6√3:3=2√3 дм
Формула радиуса окружности, описанной около правильного треугольника:
R=a/√3 =>
R=2√3:√3=2 дм
Формула стороны правильного многоугольника через радиус вписанной окружности:
а(n)=2r•tg(180°:n), где r – радиус вписанной окружности, n – число сторон,
Для правильного шестиугольника tg(180°:n)=tg30°=1/√3
a₆=2•2•1/√3=4/√3
P=6•4/√3=8√3 дм
—————
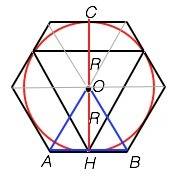
Как вариант: Правильный шестиугольник состоит из 6 равных правильных треугольников.
На рисунке приложения ОН - радиус описанной около правильного треугольника окружности и в то же время высота одного из 6 правильных треугольников, все углы которого 60°; АВ - сторона шестиугольника. Задача решается с т.Пифагора.
девятка не подходит, если разность 9. получается 9009 (не квадрат, что можно проверить на калькуляторе, используя корень)
далее разбираем поочередно каждый вариант
цифра 0 отпадает сразу, т.к. нет квадрата числа, в котором первые две цифры были бы одинаковыми, а заканчивалось бы число на два ноля
пятерка - квадрат должен заканчиваться на 25, поэтому отпадает
шестерку получаем в случаях:
9-3
8-2
7-1
6-0
в этом случае получатся такие числа: 9306 8206 7106 6006 (квадратами не являются)
по такой же схеме разбираем цифру 4..получатся: 9504 8404 6204 5104 4004(не квадраты)
разбирая цифру 1, сразу находим правильный ответ (9-8)..для проверки можно перебрать все варианты, среди которых квадратов не будет...поэтому правильный ответ:9801=99^2.