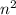коэффициент положительный, ветви параболы смотрят вверх, следовательно больше нуля заштрихованная область.
Пусть длина прямоугольника равна Х. Тогда его ширина 15 - Х
У нового прямоугольника длина Х + 5, а ширина 15 - Х - 3 = 12 - Х
Поскольку площадь прямоугольника уменьшилась на 8 см², получаем уравнение
Х * (15 - Х) - (Х + 5) * (12 - Х) = 8
15 * Х - Х² - 12 * Х + Х² - 60 + 5 * Х - 8 = 0
8 * Х - 68 = 0
Х = 8,5
Итак, длина прямоугольника была 8,5 см, ширина 15 - 8,5 = 6,5 см, а площадь 8,5 * 6,5 = 55,25 см².
После трансформации длина прямоугольника стала 8,5 + 5 = 13,5 см, ширина 6,5 - 3 = 3,5 , а площадь 13,5 * 3,5 = 47,25 см², то есть уменьшилась на 55,25 - 47,25 = 8 см².
Объяснение:Самый универсальный и могучий Функция, заданная аналитически, это функция, которая задана формулами. Собственно, это и есть всё объяснение.) Знакомые всем (хочется верить!)) функции, например: y = 2x, или y = x2 и т.д. и т.п. заданы именно аналитически.
К слову сказать, не всякая формула может задавать функцию. Не в каждой формуле соблюдается жёсткое условие из определения функции. А именно - на каждый икс может быть только один игрек. Например, в формуле у = ±х, для одного значения х=2, получается два значения у: +2 и -2. Нельзя этой формулой задать однозначную функцию. А с многозначными функциями в этом разделе математики, в матанализе, не работают, как правило.
Чем хорош аналитический задания функции? Тем, что если у вас есть формула - вы знаете про функцию всё! Вы можете составить табличку. Построить график. Исследовать эту функцию по полной программе. Точно предсказать, где и как будет вести себя эта функция. Весь матанализ стоит именно на таком задания функций. Скажем, взять производную от таблицы крайне затруднительно...)
Аналитический достаточно привычен и проблем не создаёт. Разве что некоторые разновидности этого с которыми сталкиваются студенты. Я про параметрическое и неявное задание функций.)