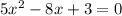Какое из уравнений является квадратным: 4x^2/ (6+x)= 0
48х^2+х^3-9=0
1-12х=0
7х^2-13х+5=0
2. В квадратном уравнении -3х^2+10х+5=0 укажите старший коэффициент:
10
5
-3
-5
3. В уравнении -6х-5х^2+9=0
Старший коэффициент равен 9, второй коэффициент равен -6, свободный член равен -5.
Старший коэффициент равен -6, второй коэффициент равен -5, свободный член равен 9.
Невозможно определить.
Старший коэффициент равен -5, второй коэффициент равен -6, свободный член равен 9.
4. Какое из квадратных уравнений является приведённым:
х^2-7х+16=0
12-х^2+3х=0
4х^2+х-1=0
-15х^2+4х-2=0
5. Какое из квадратных уравнений является неполным:
7-7х-7х^2=0
3-х^2+х=0
16х^2-9=0
–х^2-х-1=0
6. Какое из чисел является корнем квадратного уравнения 5х^2=0
-5
5
0
25
7. Какое из чисел является корнем квадратного уравнения х^2+6х+9=0:
1
3
0
-3
8. В каком из квадратных уравнений свободный член равен 0:
5х^2+2х=0
х^2-9=0
2-х-х^2=0
4х^2+5х-3=0
9. Составьте квадратное уравнение, у которого старший коэффициент равен 10, второй коэффициент равен - , свободный член равен 0,6.
10. Являются ли числа 1 и -0,6 корнями квадратного уравнения 5х^2-8х+3=0?
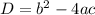 (если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена
(если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена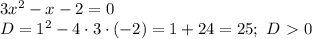
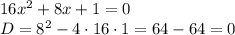


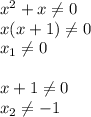
1)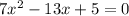 Является квадратным уравнением;
Является квадратным уравнением;
2)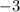 Старший коэффициент квадратного уравнения;
Старший коэффициент квадратного уравнения;
3) В квадратном уравнении Старший коэффициент равен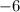 , второй коэффициент равен
, второй коэффициент равен 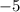 , свободный член равен
, свободный член равен 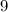
4)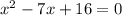 Приведённое квадратное уравнение;
Приведённое квадратное уравнение;
5)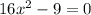 Неполное квадратное уравнение;
Неполное квадратное уравнение;
6)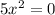
7)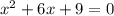
8) В квадратном уравнении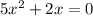 , свободный член равен
, свободный член равен 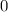
9)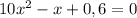
10)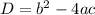
x₁ =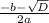
x₂ =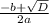
x₁ =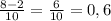
x₂ =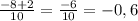
Проверка
x =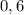
ответ подходит
Проверка
x =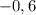
ответ не подходит
Числа и
и 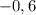 не являются корнями квадратного уравнения
не являются корнями квадратного уравнения