1. (2ab-c)(2ab+c)
Для начала, мы можем использовать формулу (a-b)(a+b) = a^2 - b^2. Применим эту формулу для первых двух скобок:
(2ab)^2 - c^2 = 4a^2b^2 - c^2
2. (4+3xy)(4-3xy)
Тут также можно использовать формулу (a-b)(a+b). Применим ее:
4^2 - (3xy)^2 = 16 - 9x^2y^2
3. (5a-3b)(5a+3b)
Опять же применим формулу (a-b)(a+b):
(5a)^2 - (3b)^2 = 25a^2 - 9b^2
Мы хотим представить степень этого одночлена.
В данном случае, степень одночлена - это число, которое показывает сколько раз нужно перемножить сам одночлен.
Чтобы решить эту задачу, мы должны умножить (3t) на само себя несколько раз в соответствии со значением степени.
В данном случае, степень одночлена равна 4, поэтому нам нужно перемножить (3t) четыре раза.
Шаг 1: Умножение одночлена на самого себя
(3t) * (3t) = (3 * 3) * (t * t) = 9t^2
На этом шаге, мы умножили коэффициенты (3 * 3) и перемножили переменные t * t, тем самым получили 9t^2.
Мы вновь умножили коэффициенты (27 * 3) и перемножили переменные t^3 * t, получив 81t^4.
Таким образом, представление степени одночлена (3t)4 равно 81t^4.
Обоснование:
При умножении одночлена на самого себя, мы добавляем показатели степени переменных.
В данном случае, у нас только одна переменная t, поэтому мы просто умножаем показатели степени.
Исходя из этого, мы пошагово умножили одночлен (3t) на самого себя четыре раза, что дало нам степень одночлена (3t)4 равную 81t^4.
Надеюсь, это объяснение понятно для школьника! Если у тебя есть еще вопросы, не стесняйся задавать.
Построим график параболы, используя направление ветвей, вершину, фокус и ось симметрии.
Направление: направлено вверх.
Вершина: ( − 3 , − 1 )
Фокус: ( − 3 ,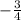 ) .
) .
Ось симметрии: x = − 3
Направляющая: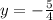
Фото таблицы и графика прикрепил.