
Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
Объяснение:
1.
Пусть скорость течения реки равна х. ⇒
Против течения реки скорость катера будет равна 25-х (км/ч),
а по течению реки скорость катера будет равна 25+х (км/ч). ⇒
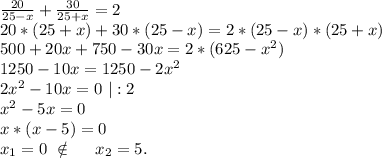
ответ: скорость течения реки 5 км/ч.
2.
Пусть скорость течения реки равна х. ⇒
Против течения реки скорость катера будет равна 25-х (км/ч),
а по течению реки скорость катера будет равна 25+х (км/ч).
Пусть время, затраченное на путь против течения реки равно t₁, а
а время, затраченное на путь по течению реки равно t₂. ⇒
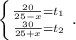
Суммируем эти уравнения:

По условию задачи на весь путь катер затратил t₁+t₂=2 (ч). ⇒
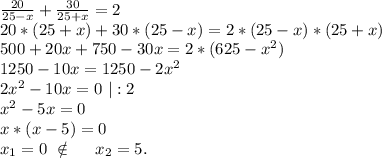
ответ: скорость течения реки 5 км/ч.
1. Пусть равное количество окуней равно х. ⇒
2. Первый рыболов поймал х+7,второй х+6, а третий х+8.
3. (x+7)+(x+6)+(x+8)=51
3x+21=51
3x=30 |:3
x=10 ⇒
ответ: первый рыболов поймал 17 окуней,
второй рыболов поймал 16 окуней,
третий рыболов поймал 18 окуней.
ответ: a) (-5)⁶
Объяснение: (-5³)²=((-5)³)²=(-5)⁶