24 см.
Объяснение:
Пусть один катет прямоугольного треугольника будет а см , а другой bсм.
Тогда площадь равна 0,5*а* b, а квадрат гипотенузы найдем по теореме Пифагора а² + b² . Так как по условию площадь равна 24 см², а гипотенуза равна 10 см , то составляем систему уравнений:
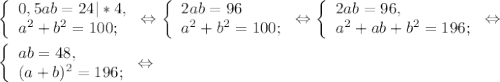

Так как a и b катеты прямоугольного треугольника , а значит положительные числа .Тогда их сумма не может быть отрицательным числом. Поэтому вторая система не подходит по смыслу задачи.
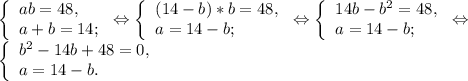
Решим квадратное уравнение:
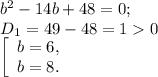
Если b=6, то а=8
Если b=8, то а=6
Значит катеты прямоугольного треугольника 6 см и 8 см. Тогда периметр ( сумма длин всех сторон треугольника)
P= 6+8+10 = 24 (см)
5
Объяснение:
Пусть на дом задано n задач, тогда всего комбинаций решенных задач 2
n
(каждую из
задач ученик может решить или не решить). Вычтем из этих комбинаций комбинации,
когда решено менее 3 задач: 1 комбинация, когда ничего не решено; n комбинаций,
когда решена 1 задача; n(n−1)
2
, когда решено две задачи (первую решенную можно
выбрать , вторую (n − 1), при этом нам не важен порядок, поэтому делим
на 2. Итого получаем, что уникальных комбинаций, за которые учитель не поставит
оценку «2»: 2
n−1−n−
n(n−1)
2
. Для того, чтобы кто-нибудь обязательно получил оценку
«2», это число должно быть меньше, чем число учеников в классе (чтобы у каких-то
двух комбинация задач совпадала). Получаем неравенство: 2
n − 1 − n −
n(n−1)
2 < 30
наибольшее n, удовлетворяющее этому неравенству это n = 5.
ответ: 5 задач
х см-сост.1 часть,тогда 2х и 3х --стороны прям-ка
2х·3х=54
6х²=54⇒х²=9,х=3(х>0)
6см и 9см --стороны пр-ка.