а)
Всего выбирать мы можем из 9+8=17 человек. Число которыми можно выбрать 7 человек из 17, равно числу сочетаний из 17 по 7:
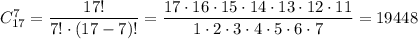
б)
Варианты, которые допустимы в таком случае:
- в бригаде 3 маляра и 4 штукатура
- в бригаде 4 маляра и 3 штукатура
- в бригаде 5 маляров и 2 штукатура
- в бригаде 6 маляров и 1 штукатур
- в бригаде 7 маляров
Например, для первого варианта:
- 3 маляра выбираются из 9 человек, поэтому число выбрать маляров равно числу сочетаний из 9 по 3
- 4 штукатура выбираются из 8 человек, поэтому число выбрать штукатуров равно числу сочетаний из 8 по 4
- выбор маляров и штукатуров независим, поэтому полученные количества нужно перемножить
Рассуждая так для каждого варианта, получим:
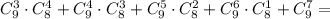
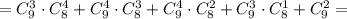
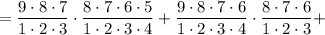
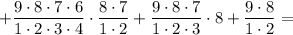

в)
Вероятность того, что в бригаде будет не менее 3 маляров, равна отношению числа которыми можно укомплектовать бригаду при условии, что в ней будет не менее 3 маляров, к общему числу укомплектовать бригаду.
Обе нужные величины уже найдены, поэтому получим:
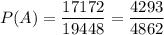
 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).


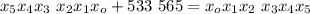 ;
;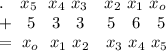

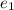 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого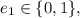
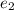 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго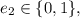
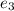 – возможная добавочная единица,
– возможная добавочная единица,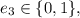
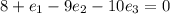 ;
;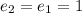 и при
и при  ;
;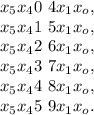
 поскольку
поскольку 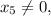 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.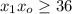 .
.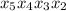 .
.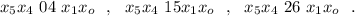
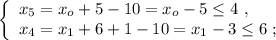

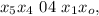
 может играть роль апреля.
может играть роль апреля.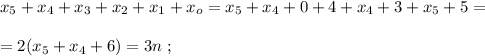
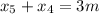 ;
;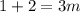 ;
;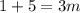 ;
;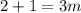 ;
; ;
;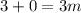 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.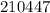 – дата 21/04/47 г.
– дата 21/04/47 г.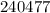 – дата 24/04/77 г.
– дата 24/04/77 г.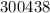 – дата 24/04/38 г.
– дата 24/04/38 г.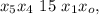
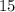 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;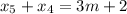 ;
;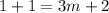 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

При делении показатели степени вычитаются
m^(8-3-2)
m^3 - остаётся
а) 3^3 = 27
б) 10^3 = 1000
в) -2^3 = (-8)
г) 1/7^3 = 1/343
"^" - знак возведения в степень