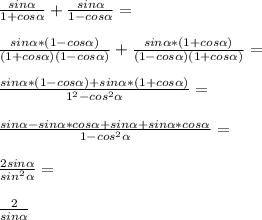
альфа = х
Дано
sinx/(1+cosx) + sinx/(1 - cosx)
Приведём к общему знаменателю (1 - cosx)(1 + cosx) домножим на сомножители
(1-сosx)*sinx/(1+cosx) + (1+cosx)*sinx/(1 - cosx) В Знаменателе будет (1 - cosx)(1 + cosx) = 1 - cos^2 (x) = sin^2 (x) раскроем скобки в числителе (sinx - cosxsinx + sinx +cosxsinx )/ sin^2 (x) 2sinx/ sin^2 (x) = 2/sinx
1.
а)x^3-2x = х(х²-2)
б)5a^2-10ab+5b^2 = 5(a^2-2ab+b^2) = 5(a-b)²
в)cm-cn+3m-3n = (cm-cn)+(3m-3n) = с(m-n)+3(m-n) = (с+3)(m-n)
2.
2(p+q)²-p(4q-p)+q² = 3p²+3q² при любых p и q
2(p+q)²-p(4q-p)+q² = 2(p²+2pq+q²) -4pq+p²+q² = 2p²+4pq+2q² -4pq+p²+q² = 3p²+3q²
таким образом, мы привели левую часть к правой, тем самым доказав, что значения выражений будут равны при любых p и q
3.
(x-3)(x+3) = x(x-2)
х²-9=х²-2х
2х=9
х=4,5
ответ: при х=4,5
4.
а)(a-3b)(a+3b)+(2b+a)(a-2b) = (a²-9b²) + (a²-4b²) = 2a²-13b²
б)(p+q)(q-p)(q²+p²) = (q²-p²)(q²+p²) = q⁴-p⁴
5.
x³-27-3x(x-3)=0
(x³-3³)-3x(x-3)=0
воспользуемся формулой разности кубов:
(х-3)(х²+3х+9)-3x(x-3)=0
(х-3)(х²+3х+9-3х)=0
х-3=0 или (х²+3х+9-3х)=0
х=3 х²+9=0
х²=-9 - решений нет
ответ: х=3
ответ: 3) ВС1=6 4) С=НВА=30 А=СВН=60
Объяснение: 3)Угол АВС=180-(60+80)=40 СС1-биссектриса АСВ, значит угол ВСС1=ВСА/2=80/2=40 ВСС1=СВС1, т.е. треуг. ВСС1 равнобедрен. с основанием ВС, т.е. ВС1=СС1=6
4) по т.синусов Стороны треугольника пропорциональны синусам противолежащих углов. 16/sinB=8/sinC=8√3/sinA
AC^2=AB^2+BC^2 (т.Пифагора) BC^2=16^2-8^2=192 BC=8√3
угол В=90, а sin90=1 16/1=8√3/sinA sinA =8√3/16=√3/2 угол А=60, значит угол С=180-(90+60)=30
Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному. угол С=НВА=30 А=СВН=60