Question

Sin 18 (с тригонометрии) с подробным описанием решение защитаю если полностью объясните вот это решение sin 36°= cos 54°= cos (18° + 36°); 2 sin18° cos18° = cos18° cos36° – sin18° sin36°; 2 sin18° cos18°= cos18°(1 – 2sin218°) – 2sin218°cos18° 2 sin18° = 1 – 4sin218°, решаем квадратное уравнение и учтем, что sin18° > 0, получим sin18° = .(корень5-1)/4

Answer 1

по формуле приведения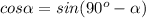 $cos \alpha=sin (90^o-\alpha)$

$sin 36^o=sin(90^o-54^o)=cos 54^o$

так как 18+36=54, то

$cos (54^o)=cos(18^o+36^o)$

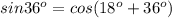т.е. $sin 36^o=cos (18^o+36^o)$ (1)

по формуле синуса двойного угла(аргумента)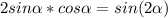 $2sin \alpha*cos \alpha=sin (2 \alpha)$

$sin 36^o=2*sin 18^o*cos 16^o$ (2)

по формуле косинуса суммы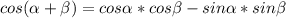 $cos (\alpha+ \beta)=cos \alpha *cos \beta -sin \alpha* sin \beta$:

$cos (18^o+36^o)=cos 18^ocos 36^o-sin 18^osin 36^o$ (3)

Подставив (2) и (3) в (1) получим

$2sin 18^o cos 18^o=cos 18^ocos 36^o-sin 18^osin 36^o$ (4)

используя формулы синуса двойного угла (выше упоминалась) и косинуса двойного угла

$cos (2 \alpha)=1-2sin^2 \alpha$

имеем что

$cos 18^o cos 36^o-sin 18^osin 36^o=\\\\cos 18^o(1-2sin^2 18^o)-sin 18^o*2sin 18^o*cos18^o =cos 18^o(1-2sin 18^o)-2cos 18^0 sin^2 18^o$ (5)

Подставляя (5) в (4), упращая и сокращая обе части равенства на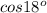 $cos 18^o$

$2sin 18^o *cos 18^o=cos 18^o(1-2sin 18^o)-2cos 18^0sin^2 18^o;\\\\2sin 18^o=1-2sin18^o-2sin^2 18^o;\\\\2sin 18^o=1-4sin^2 18^o$ (6)

Получили квадратное уравнение относительно sin 18

$4sin^2 18^o+2sin 18^o-1=0;\\\\D=2^2-4*4*(-1)=4+16=20=4*5=2^2*5;\\\\sin_1 18^0=\frac{-2-2\sqrt{5}}{2*4}=\frac{-1-\sqrt{5}}{4}$

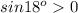так как $sin 18^o0$, как синус острого угла (т.е. угла большег 0 градусов и меньшего 90 градусов)

Как-то так*