6-3x<4-5x
2x<-2
x<-1
x e (-бесконечности; -1)
21-2x<=6-5x
3х <= -15
х <= -5
x e (-бесконечности ; -5];
Общее решение будет пересечение двух промежутков
-5 -1
>
Общий ответ: (-бесконечности; -5]
![lim_{x\to \infty }\frac{x+1}{x-2}=lim_{x\to \infty }\frac{\frac{x}{x}+\frac{1}{x}}{\frac{x}{x}-\frac{2}{x}}=lim\frac{1+\frac{1}{x}}{1-\frac{2}{x}}=[\frac{1+0}{1-0}]=\frac{1}{1}=1](/tpl/images/0237/6916/b2fde.png)
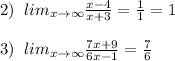
![lim_{x\to \infty }\frac{x+3}{5x^2+2x-5}=0,tak\; \; kak\\\\lim_{x\to \infty }\frac{\frac{x}{x^2}+\frac{3}{x^2}}{\frac{5x^2}{x^2}+\frac{2x}{x^2}-\frac{5}{x^2}}=lim\frac{\frac{1}{x}+\frac{3}{x^2}}{5+\frac{2}{x}-\frac{5}{x^2}}=[\frac{0+0}{5+0-0}]=\frac{0}{5}=0](/tpl/images/0237/6916/32e6e.png)
х ∈ [ -6; -5)
Объяснение:
для более понятного решения, поскольку уравнение обычно представляют в виде
ах² +bx +c =0, а у нас тоже есть а, то мы обозначим уравнение так
a'x² +bx +c = 0
тогда наше а останется как а
теперь решение
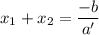
поскольку корни должны быть отрицательные,
то -b/a' должно быть <0

это первое условие
теперь второе
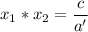
поскольку оба корня должны быть отрицательны, их произведение должно быть положительно
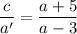
поскольку у нас (а-3) < 0 (знаменатель) по первому условию, то для получения положительной дроби числитель тоже должен быть <0
a +5 < 0 ⇒ a < -5 это второе условие.
и теперь проверим вершину параболы, чтобы она была выше оси ох и ветвями вниз
координата вершины по y
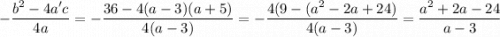
и вот это должно быть ≥0
а поскольку у нас (а-3) <0, то для получения положительной дроби мы рассмотрим числитель ≤0
a² +2a -24 ≤ 0 ⇒ -6 ≤ x ≤4 и это наше третье условие
и вот теперь объединим все три условия и получим ответ
-6 ≤ x < -5
ответ
х ∈ [ -6; -5)
6-3x<4-5x
-3x+5x<-6+4
2x<-2 (:2)
x<-1
хэ минус бесконечности до -2
21-2x<6-5x
-2x+5х<6-21
3х<-15
х<-5
хэ от минус бесконечности до -5
Общее решение:
хэ от минус бесконечности до -5
Думаю, что так . Я только попыталась