30 кг
Объяснение:
Пусть «
» кг раствора было изначально ⇒ 
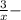доля соли в этом растворе ⇒ 
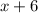кг раствора стало после добавления соли ⇒ 
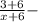доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (
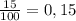), получим:
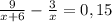
Домножим обе части уравнения на и 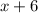, получим:
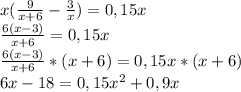
Перенесём правую часть уравнения в левую, получим:
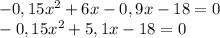
Квадратное уравнение вида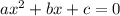 
можно решить с дискриминанта 
.
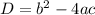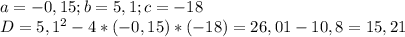
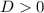⇒ корней будет два.
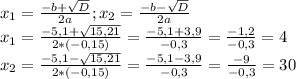
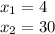
По условию концентрация соли в первоначальном растворе была меньше 20% ⇒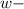 
(массовая доля соли в первоначальном растворе) должна быть 
.
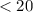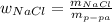* 100%
⇒ 
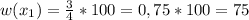
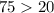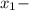не является решением.
⇒ 
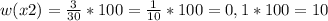
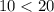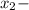является решением.
Значит, первоначальная масса раствора была 30 кг.
Тогда x/34 ч. - время, за которое проехал автомобиль эту половину (ведь время равно расстоянию делить на скорость).
Вторая половина пути имеет ту же длину х км. (она ведь половина, как и первая). Поэтому ее автомобиль проехал за x/51 часов.
Средняя скорость движения, по определению, равна общему пройденному пути (который равен 2х км) делить на общее затраченное время, которое равно x/34+x/51 часов.
Итак, средняя скорость равна
2x/(x/34+x/51)=2*34*51x/(51x+34x)=2*34*51/85=40,8 км/ч.
В решении не понадобилось находить расстояние х, оно благополучно сократилось при нахождении средней скорости.