А1. Найдите производную функции: а) х5+2х; б) 12х6 - 45; в) 22 хх
; г) 32 4 х3 .
А2. Найдите производную функции а) (х2 -3)(х+х3); б) х
5 х 2 .
х 1
А3. При каких значениях х значение производной функции f(x = х5+2,5х4-12
равно 0?
В1. Найдите значения х , при которых значение производной функции
f (x) 6х х
х положительно.
х
В2. Найдите производную функции у х
2 .
C1. При каких значениях х производная функции у 5 3х 4 3х 13 принимает
отрицательные значения ?
С2. Найдите производную функции f (x) х2 8х 7 при 1

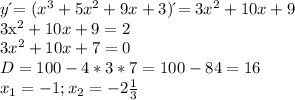

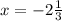
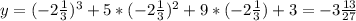
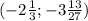 :
: (НЕТ)
(НЕТ)
Левая часть определена при
-1≤3x+2≤1,
-3≤3x≤-1
-1≤x≤-1/3, т.е. х∈[-1;-1/3].
Правая часть определена при
-1≤4x²+x≤1
Решаем 4x²+x-1≤0: x1=(-1-√17)/8≈-0,64; x1=(-1+√17)/8≈0,39, т.е. x∈[x1;x2]
Решаем 4x²+x+1≥0: D<0, х∈(-∞;+∞)
Итак, нам надо найти решения неравенства на интервале
[(-1-√17)/8;-1/3].
Воспользуемся тем, что если функция f убывает на некотором интервале, то неравенство f(а)<f(b) равносильно неравенству a>b для любых а и b из этого интервала, т.е. неравенство f(3x+2)<f(4x²+x) равносильно неравенству
3x+2>4x²+x
Решаем его:
4x^2-2x-2<0
2x²-x-1<0
x1=-1/2, x2=1
x∈(-1/2;1)
Итак, x∈(-1/2;1)∩[(-1-√17)/8;-1/3]=(-1/2;-1/3], т.к. (-1-√17)/8≈-0,64<-1/2.
ответ: x∈(-1/2;-1/3].