Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии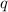 
должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
Графически это выглядит так: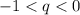 
или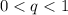 
.
Рассмотрим наши примеры:
1) 
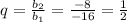. Выполняются ли условия неравенства?
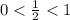. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
2) 
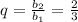. Выполняются ли условия неравенства?
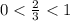. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
3) 
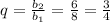. Выполняются ли условия неравенства?
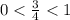. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
Объяснение:
Пусть х - скорость теплохода в неподвижной воде, тогда его скорость по течению равна х+4, а против течения х-4.
Время движения по течению 384/(х+4), время движения против течения 384/(х-4))
Составим уравнение 384/(х+4) +384/(х-4) + 8 = 48
96/(х+4) +96/(х-4) = 10
96х - 96*4 + 96х +96*4 = 10(х^2-16)
10 x^2 - 192x - 160 = 0
5 x^2 - 96x - 80 = 0
D =96^2 +4*80*5 = 9216 + 1600 = 10816, sqrt(D) = 104
x1 = (96+104)/10 = 20
x2 = (96-104)/10 <0 отрицательной скорости не может быть
ответ: скорость теплохода в неподвижной воде равна 20км/ч
1) x^5 + 3x^3 + 2x = 0
x(x^4 + 3x^2 + 2) = 0
x(x^2 + 1)(x^2 + 2) = 0
Скобки (x^2 + 1) и (x^2 + 2) > 0 при любом х, поэтому
ответ: x = 0
2) 2x^3 - x^2 - 2x + 1 = 0
x^2*(2x - 1) - (2x - 1) = 0
(2x - 1)(x^2 - 1) = 0
(2x - 1)(x - 1)(x + 1) = 0
ответ: x1 = 1/2; x2 = 1; x3 = -1