Алгебра: ДАЮ 30 б. РЕШИТЕ как в файле.

ДАЮ 30 б. РЕШИТЕ как в файле.

👇

Открыть все ответы

Ответ:

Юлия19112006

24.12.2020

$4)\ \ \sum \limits _{n=1}^{\infty }\dfrac{1}{n(n+1)}=\sum \limits _{n=1}^{\infty }\dfrac{1}{n^2+n}\\\\\\Neobxodimuj\ priznak:\ \lim\limits _{n \to \infty} a_n=\lim\limits _{n \to \infty}\dfrac{1}{n^2+n}=0\ \ \Rightarrow \ \ ???$

Если предел общего члена ряда равен 0, то ответ о сходимости ряда дать невозможно. Поэтому ряд надо исследовать с других признаков. (Вот если бы предел общего члена ряда не был = 0, то вывод можно было бы сделать однозначно, ряд бы расходился.)

Применим признак сравнения:

$a_{n}=\dfrac{1}{n^2+n}$

По признаку сравнения: мажорантный ряд сходится, значит сходится и минорантный ряд ⇒ исходный ряд сходится .

$6)\ \ \sum \limits _{n=1}^{\infty }\dfrac{1}{n}\cdot tg\dfrac{\pi}{3n}\\\\Neobx.\; priznak:\ \lim\limits _{n \to \infty} a_n= \lim\limits _{n \to \infty}\frac{1}{n}\cdot tg\frac{\pi}{3n}=\Big[0\cdot 0\; \Big]=0\ \ \Rightarrow \ \ \ ???\\\\sinx$

$tg\dfrac{\pi}{3n}\dfrac{\pi}{3n}\ \ (n\to +\infty )\ \ \Rightarrow \ \ \ a_{n}=\dfrac{1}{n}\cdot tg\dfrac{\pi}{3n}\dfrac{1}{n}\cdot \dfrac{\pi}{3n}=\dfrac{\pi}{3n^2}=b_{n}\ -\ sxoditsya\; ,\\\\tak\ kak\ \ \sum \limits _{n=1}^{\infty }\dfrac{1}{n^2}\ -\ sxoditsya$

Получили, что сходится минорантный ряд, а из этого факта не следует сходимость мажорантного ряда. Поэтому применим признак сравнения в предельной форме.

$\lim\limits _{n \to \infty}\dfrac{a_{n}}{b_n}=\lim\limits _{n\to \infty }\dfrac{\frac{1}{n}\cdot tg\frac{\pi}{3n}}{\frac{1}{n^2}}=\lim\limits _{n\to \infty }\dfrac{\frac{1}{n}\cdot \frac{\pi}{3n}}{\frac{1}{n^2}}=\dfrac{\pi }{3}\ne 0\ \ \Rightarrow$

Оба ряда ведут себя одинаково, то есть сходятся .

$8)\ \ \sum \limits _{n=1}^{\infty }3^{n}\cdot sin\dfrac{\pi}{4^{n}}\\\\sin\dfrac{\pi}{4^{n}}$

$\lim\limits _{n \to \infty}\dfrac{a_n}{b_{n}}= \lim\limits _{n \to \infty}\dfrac{3^{n}\cdot sin\frac{\pi}{4^{n}}}{(3/4)^{n}}= \lim\limits _{n \to \infty}\frac{3^{n}\cdot (\pi/4^{n})}{(3/4)^{n}}=\pi \ne 0\ \ \Rightarrow$

Оба ряда ведут себя одинаково, то есть сходятся .

$7)\ \ \sum\limits _{n=1}^{\infty }\, ln\dfrac{n+3}{n+2}\\\\ln\dfrac{n+3}{n+2}=ln\Big(1+\dfrac{1}{n+2}\Big)\sim \dfrac{1}{n+2}\ \ \ (n\to \infty )\ \Rightarrow \\\\\sum\limits _{n=1}^{\infty }\, b_{n}=\sum\limits _{n=1}^{\infty }\dfrac{1}{n+2}\ -\ rasxoditsya\\\\\\\lim\limits _{n \to \infty}\dfrac{a_n}{b_{n}}=\lim\limits _{n \to \infty}\dfrac{ln(1+\frac{1}{n+2})}{\frac{1}{n+2}}= \lim\limits _{n \to \infty}\dfrac{\frac{1}{n+2}}{\frac{1}{n+2}}=1\ne 0\ \ \Rightarrow$

Оба ряда расходятся .

$11)\ \ \sum\limits _{n=1}^{\infty }\, \dfrac{2^{n}}{4^{n}+7}\\\\a_{n}=\dfrac{2^{n}}{2^{2n}+7}$

Оба ряда сходятся .

4,4(24 оценок)

Ответ:

uylia7

24.12.2020

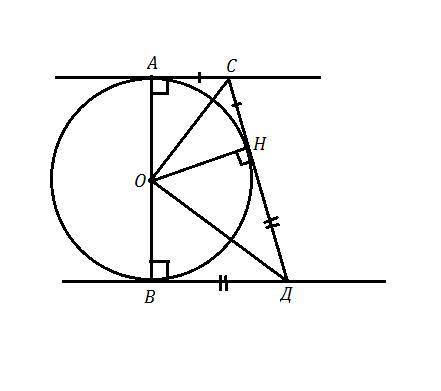
Задана окружность с центром в точке О , АВ - диаметр ,

АС и ВД - касательные к окружности, точки А и В - точки касания.

Радиус окружности, проведённый в точку касания перпендикулярен касательной ⇒ АО⊥АС и ВО⊥ВД .

СД - касательная, точка Н - точка касания ⇒ ОН⊥СД .

Получили четырёхугольник АСДВ - прямоугольная трапеция.

АС=СН и ВД=ДН , так как отрезки касательных к окружности, проведенных из одной точки, равны . ОА=ОН=ОВ как радиусы окружности, СО - общая ⇒ ΔАОС=ΔНОС , ΔВОД=ΔНОД по трём сторонам ⇒ ∠АСО=∠НСО, значит СО - биссектриса.

Рассмотрим ΔСОД. ∠СОД=90°, т.к. ∠ДСО+∠СДО=(∠С+∠Д ):2=90°

ОН - высота, опущенная из прямого угла есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой, то есть ОН²=СН*ДН , но СН=СА и ДН=ДВ, значит

ОН²=СА*ДВ