. Любое число можно представить в виде произведения простых множителей. Запишем:
, где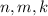 
- некоторые натуральные числа.
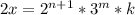является полным квадратом, значит 
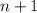и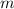 
- четные числа, а 
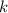- полный квадрат. Аналогично, число 
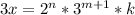является полным кубом, значит 
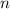и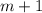 
делятся на 3, а 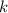- полный куб. 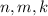это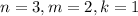 
, значит 
.
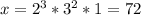Модуль раскрывается так:
у=-3х-3, если 3х+3>0
y=3x+3, если 3х+3<0
y=0, если 3х+3=0
Отсюда у=-3х-3, если х>-1
y=3x+3, если х<-1
y=0, если х=-1